题目内容
【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高![]() 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心![]() 米.
米.

(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
【答案】(1)y=-![]() (0≤x≤3);(2)抛物线水柱的最大高度为
(0≤x≤3);(2)抛物线水柱的最大高度为![]() m.
m.
【解析】
试题分析:(1)以水管和地面交点为原点,原点与水柱落地点所在直线为x轴适当的直角坐标系,利用顶点式y=a(x-1)2+k,求解析式
(2)利用顶点式y=-![]() (x-1)2+
(x-1)2+![]() (0≤x≤3),知顶点坐标(1,
(0≤x≤3),知顶点坐标(1,![]() ),从而求出水柱的最大高度是
),从而求出水柱的最大高度是![]() 米。
米。
试题解析:(1)如图,以水管与地面交点为原点,原点与水柱落地点所在直线为x轴,水管所在直线为y轴,建立平面直角坐标系.
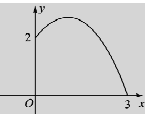
由题意可设抛物线的函数解析式为y=a(x-1)2+h(0≤x≤3)
抛物线过点(0,2)和(3,0),代入抛物线解析式得:
![]()
解得: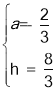
所以,抛物线的解析式为:y=-![]() (x-1)2+
(x-1)2+![]() (0≤x≤3),
(0≤x≤3),
化为一般形式为:y=-![]() (0≤x≤3)
(0≤x≤3)
(2)由(1)知抛物线的解析式为y=-![]() (x-1)2+
(x-1)2+![]() (0≤x≤3),
(0≤x≤3),
当x=1时,y=![]() ,
,
所以,抛物线水柱的最大高度为![]() m.
m.

练习册系列答案
相关题目