题目内容
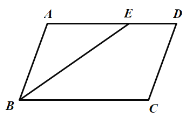
【题目】如图1,将![]() 沿
沿![]() 翻折,点
翻折,点![]() 的对称点是点
的对称点是点![]() ,
,![]() ,
,
(1)求证:四边形![]() 是菱形;
是菱形;
(2)如图2,在![]() 上取一点
上取一点![]() ,连接
,连接![]() 并延长至点
并延长至点![]() ,在
,在![]() 上取一点
上取一点![]() ,连接
,连接![]() ,若
,若![]() ,求证:
,求证:![]() .
.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据翻折前后对应边相等,对应角相等,再结合平行线的性质可证AB=BC,所以四边形四条边相等,由此可证;
(2)根据三角形内角和定理和三角形外角定理对等式的左右两边进行化简可得![]() ,从而证明结论.
,从而证明结论.
解:(1)∵![]() 沿
沿![]() 翻折,
翻折,
∴AB=AD,BC=CD,∠BAC=∠DAC,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠BAC=∠ACB,
∴AB=BC,
∴AB=BC=CD=AD,
∴四边形ABCD为菱形;
(2)∵∠BAC=∠ACB,
∴∠EBC+∠BAC=∠EBC+∠ACB=∠AEB,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下面的频数分布
次数 | 60≤x<80 | 80≤x<100 | 100≤x<120 |
频数 | 1 | 2 | 25 |
次数 | 120≤x<140 | 140≤x<160 | 160≤x<180 |
频数 | 15 | 5 | 2 |
(1)全班有多少学生?
(2)组距是多少?组数是多少
(3)跳绳次数x在100≤x<140范围的学生占全班学生的百分之几?
(4)画出适当的统计图表示上面的信息.
(5)你怎样评价这个班的跳绳成绩?