题目内容
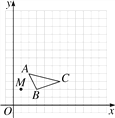
【题目】在13×13的网格图中，已知△ABC和点M(1，2)．
(1)以点M为位似中心，画出△ABC的位似图形△A′B′C′，其中△A′B′C′与△ABC的位似比为2；
(2)写出△A′B′C′的各顶点坐标．
【答案】（1）画图见解析；
(2)△A′B′C′的各顶点坐标分别为A′(3，6)，B′(5，2)，C′(11，4)．
【解析】试题分析：（1）延长MA到A′使AA′=MA，则点A′为A的对应点，同样方法作出B、C的对应点B′、C′，从而得到△A′B′C′；
（2）利用（1）所画图形可得到△A′B′C′的各顶点坐标；
（3）先把位似中心M平移到原点，则点P平移后所得对应点为（a﹣1，b﹣2），则以O点为位似中心，位似比为2，点（a﹣1，b﹣2）的对应点为（2a﹣2，2b﹣4），然后把点（2a﹣2，2b﹣4）向右平移1个单位，向上平移2个单位即可得点P′的坐标．
解：（1）如图，△A′B′C′为所作；
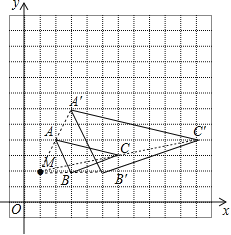
（2）A′（3，6），B′（5，2），C′（11，4）；
（3）点P（a，b）在△ABC内，则点P的对应点P′的坐标为（2a﹣1，2b﹣2）．
故答案为（2a﹣1，2b﹣2）．
练习册系列答案
阅读快车系列答案
相关题目
