题目内容
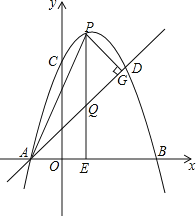
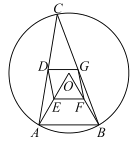
【题目】如图,![]() 是半径为4的
是半径为4的![]() 的内接三角形,连接
的内接三角形,连接![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.
(1)试判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(2)填空:①若![]() ,当
,当![]() 时,四边形
时,四边形![]() 的面积是__________;②若
的面积是__________;②若![]() ,当
,当![]() 的度数为__________时,四边形
的度数为__________时,四边形![]() 是正方形.
是正方形.
【答案】(1)四边形![]() 是平行四边形,见解析;(2)①6,②75°或15°.
是平行四边形,见解析;(2)①6,②75°或15°.
【解析】
(1)利用中位线性质,中位线平行于第三边并且等于第三边的一半,只要证明DG=EF,DG∥EF即可解决问题;
(2)①只要证明四边形DEFG是矩形即可解决问题;
②分点C在优弧AB或劣弧AB上两种情形讨论即可.
解:
⑴四边形![]() 是平行四边形.
是平行四边形.
∵点![]() 分别是
分别是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形;
是平行四边形;
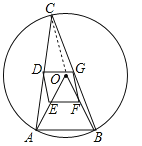
(2)①连接![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ,同理
,同理![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴四边形![]() 的面积=
的面积=![]() ,故答案为6;
,故答案为6;
②当![]() 是优弧
是优弧![]() 的中点时,四边形
的中点时,四边形![]() 是正方形,此时
是正方形,此时![]() ,
,
当![]() 是劣弧
是劣弧![]() 的中点时,四边形
的中点时,四边形![]() 是正方形,此时
是正方形,此时![]() ,故答案为75°或15°.
,故答案为75°或15°.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目