题目内容
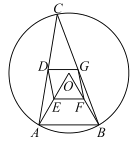
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 的中点,过点
的中点,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 的外接圆与边
的外接圆与边![]() 交于点
交于点![]() ,
,![]() ,
,
(1)①补全图形;②判断直线![]() 与
与![]() 的外接圆的公共点个数,并给出证明.
的外接圆的公共点个数,并给出证明.
(2)若![]() ,
,![]() ,求线段
,求线段![]() 的长度.
的长度.
【答案】(1)①见解析;②1个,证明见解析;(2)3
【解析】
(1)①△ADC是直角三角形,则斜边AC的中点即为外接圆的圆心;
②利用等腰三角形ABC和等腰三角形ODC角度的关系,推导出∠ODE=90°,证OD与圆相切;
(2)如下图,连接CF,则DE是△BCF的中位线,在Rt△AFC中,利用三角函数关系表示出AF、FC、AC之间的长度关系,结合BE的长度可求得
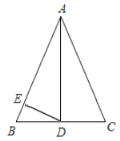
(1)①图像如下,取AC的中点O,以OA为半径作圆,圆AB交于点F
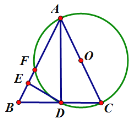
②如下图,连接OD
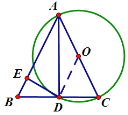
∵△ADC是直角三角形,点O是AC的中点
∴OA=OD=OC
∴∠ODC=∠OCD
∵AB=AC
∴∠ABC=∠ACB,∴∠ABC=∠ACB=∠ODC
∵DE⊥AB,∴∠BED=90°,∴∠EBD+∠EDB=90°
∴∠EDB+∠ODC=90°,∴∠EDO=90°
∴ED与圆O相切,所以有1个交点
(3)如下图,连接CF
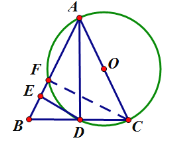
∵AC是圆O的直径,∴∠AFC=90°
又∵∠DEB=90°,∴DE∥CF
∵AB=AC,AD⊥BC,∴BD=DC
∴DE是△BCF的中位线
∵BE=1,∴EF=1
∵cos∠BAC=![]()
∴在Rt△ACF中,设AF=3x,则AC=5x,
∴AB=5x,∴BF=2x=2,∴x=1
∴AF=3

【题目】某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.假定每位顾客购买商品的可能性相同.
商品 顾客人数 | 甲 | 乙 | 丙 | 丁 |
100 | √ | × | √ | √ |
217 | × | √ | × | √ |
200 | √ | √ | √ | × |
300 | √ | × | √ | × |
85 | √ | × | × | × |
98 | × | √ | × | × |
(1)估计顾客同时购买乙和丙的概率为__________.
(2)如果顾客购买了甲,并且同时也在乙、丙、丁中进行了选购,则购买__________(填乙、丙、丁)商品的可能性最大.