题目内容
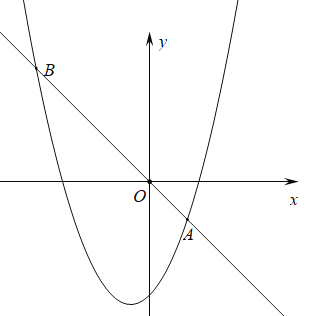
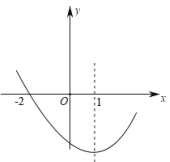
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交点
轴交点![]() ,抛物线
,抛物线![]() 经过
经过![]() ,
,![]() 两点,与
两点,与![]() 轴交于另一点
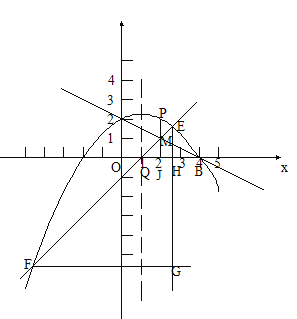
轴交于另一点![]() .如图1,点
.如图1,点![]() 为抛物线上任意一点,过点
为抛物线上任意一点,过点![]() 作
作![]() 轴交
轴交![]() 于
于![]() .
.
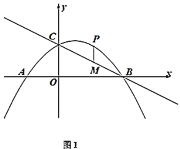
(1)求抛物线的解析式;
(2)当![]() 是直角三角形时,求
是直角三角形时,求![]() 点坐标;
点坐标;
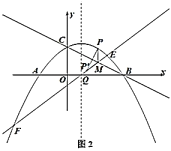
(3)如图2,作![]() 点关于直线
点关于直线![]() 的对称点
的对称点![]() ,作直线
,作直线![]() 与抛物线交于
与抛物线交于![]() ,设抛物线对称轴与
,设抛物线对称轴与![]() 轴交点为
轴交点为![]() ,当直线
,当直线![]() 经过点
经过点![]() 时,请你直接写出
时,请你直接写出![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3) 2
;(3) 2![]() .
.
【解析】
(1)先求出A、C点的坐标,然后用待定系数法确定抛物线的解析式即可;
(2)设![]() ,则
,则![]() ,然后就P在BC上方和下方分别解答即可;
,然后就P在BC上方和下方分别解答即可;
(3)由题意得B、C两点的坐标分别为(4,0)和(0,2),求得M和Q的坐标,得出直线QM的解析式,进而确定E、F两点的横坐标和纵坐标;然后过点E做垂直于x轴的直线交点为H,过点F做垂直于y轴的直线,交于点G ,证得△EQH∽△EFG和△MQJ∽△EQH,然后运用相似三角形的性质列出方程解答即可.
解:(1)在![]() 中,当
中,当![]() 时
时![]() ,当
,当![]() 时
时![]() ,∴
,∴![]() 、
、![]()
∵抛物线![]() 的图象经过
的图象经过![]() ,
,![]() 两点
两点
∴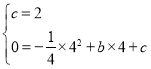
∴![]()
∴抛物线的解析式为![]()
(2)设![]() ,则
,则![]()
①当![]() 在
在![]() 的上方时,
的上方时,
![]() ,
,![]()
若![]() ,
,
∵![]() 轴,可得
轴,可得![]() 轴
轴
∴![]()
∴![]()
在![]() 中
中![]()
∴在![]() 中,
中,![]()
∴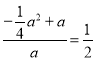
∴![]() 或
或![]() (舍去)
(舍去)
∴![]() 点坐标
点坐标![]()
②当![]() 在
在![]() 的下方时,过
的下方时,过![]() 作
作![]() 于
于![]() .
.
若![]() ,
,![]()
![]()
![]()
∴![]()
∴在![]() 中,
中,![]()
∴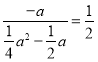 .
.
∴![]() 或
或![]() (舍去)
(舍去)
∴![]() 点坐标
点坐标![]()
∴当![]() 是直角三角形时,
是直角三角形时,![]() 点坐标为
点坐标为![]() 或
或![]() .
.
(3)设BC直线为y=kx+b,
有![]() 解得导
解得导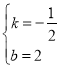 ,
,
∴直线BC为![]()
抛物线的解析式可化为:![]() ,
,
∴点Q坐标为(1,0)
∵PM⊥x轴
∴点M横坐标即为点P横坐标,为2
又∵点M在直线BC上,有![]() =1
=1
∴点M坐标为(2,1)
设过点Q、M直线为y=k2x+b2,
则有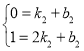 ,解得
,解得
∴ QM直线为y=x-1
由 解得
解得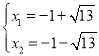
∴E、F横坐标别为Ex=![]() ,Fx=
,Fx=![]()
又∵点E、F在QM直线上,
∴点E、F别坐标为Ey=![]() ,Fy=
,Fy=![]()
过点E作垂直于x轴的直线交点为H,过点F作垂直于y 轴的直线,交于点G
∵EH⊥x轴,FG⊥y轴
∴EH⊥FG,G点坐标为(Ex,Fy)
∴∠EHQ=∠EGF=90°
又∵∠EQH=∠EFG
△EQH∽△EFG
过点M作垂直于x轴的直线交点为J
同理可得△MQJ∽△EQH,
∴△EQH∽△EFG△MQJ,
∴![]()
∴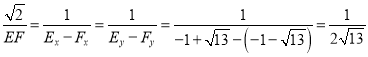
∴EF=![]() ×
×![]() =2
=2![]()