Question

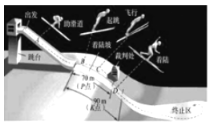
【题目】跳台滑雪是冬季奥运会比赛项目之一，如图平面直角坐标系是跳台滑雪的截面示意图，运动员沿滑道下滑，在轴上的点起跳，点距落地水平面轴，运动员落地的雪面开始是一段曲线，到达点后变为水平面，点距轴的水平距离为．运动员（看成点）从点起跳后的水平速度为，点是下落路线的某位置．忽略空气阻力，实验表明：，的竖直距离与飞出时间的平方成正比，且时；，的水平距离是米．

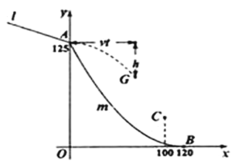
（1）用含的代数式表示；

（2）用含、的代数式表示点的横坐标和纵坐标，并求与的关系式（不写的取值范围）；

（3）奥运组委会规定，运动员落地点距起跳点的水平距离为运动员本次跳跃的成绩，并且参赛的达标成绩为．在运动员跳跃的过程中，点处有一个摄像头，记录运动员的空中姿态，当运动员飞过点时，在点上方可被摄像头抓拍到．若运动员本次跳跃达到达标成绩，并且能被处摄像头抓拍，求从点起跳后的水平速度的取值范围．

Answer 1

【答案】（1）；（2）；（3）.

【解析】

（1）设，根据时，求出k=5，由此得到答案；

（2）由题意得， ，根据由题意得得到，代入函数解析式；

（3）由时，求出或（舍去），解得，根据x=100时，解得，由此得到答案.

（1）设，

∵时，

∴k=5，

∴；

（2）由题意得， ，

∵，

∴，

∴；

（3）∵，

∴当时，，

解得或（舍去），

由题意可知解得，

当时，，

解得由二次函数图象及的实际意义可知，，

∵，

∴.