Question

【题目】如图，已知二次函数的图象与轴交于点，，与轴交于点，连接，，为线段上一点，于点，轴交抛物线于点．

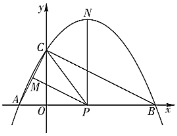
（1）求二次函数的解析式；

（2）①当为等腰三角形时，求点的坐标；

②求的最大值；

（3）直接写出当面积最大时，点的坐标．

Answer 1

【答案】（1）；（2）①点的坐标为或；②；（3）

【解析】

（1）已知抛物线上点的坐标，用待定系数法即可得出抛物线解析式．

（2）①已知B、C点坐标，求出BC，根据等腰三角形性质，当时，即可求出点P坐标；当时，过点作．设，则，根据勾股定理求出t，即可求出P点坐标．

②已知抛物线解析式，可求得A点坐标，根据勾股定理可验证是直角三角形．设点的坐标为，则，由，可将PM和PN用t表示出来，是关于t的二次函数，根据二次函数性质可求出最大值．

（3）过点作轴于点，点的坐标为，

证明△AMP∽△ACB，，得出，，得出关于t的一元二次方程，根据函数性质，得出当t=3时，面积有最大值，再求出P点坐标．

解：（1）二次函数的图象与轴交于点，，与轴交于点，

∴

解得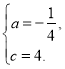

∴抛物线的解析式为．

故答案为：

（2）①∵，，

∴．

当时，．

∴点的坐标为；

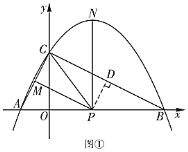
当时，如图①，过点作．设，则．

∴．解得．

此时点的坐标为．

综上，当为等腰三角形时，点的坐标为或．

②令，则．

解得，．

∴点的坐标为．

∴，．又，

∴是直角三角形．

∵，

∴．

设点的坐标为，则，

∴，．

∴．

∴的最大值为．

故答案为：或；

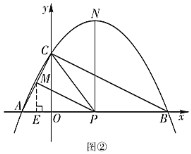
（3）如图②，过点作轴于点，点的坐标为，

∵PM∥BCM，∠APM=∠ABC

∴ △AMP∽△ACB

∴

∴

∴．

∵∴当时，的最大面积是5．

∴点的坐标为．

故答案为：P