题目内容
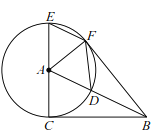
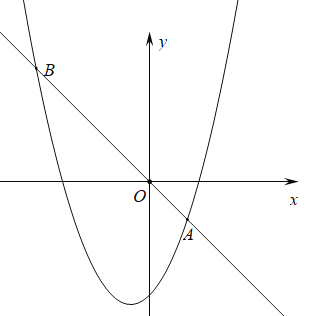
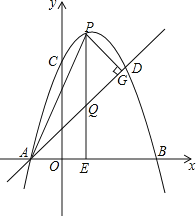
【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),C(0,3)两点,点B是抛物线与x轴的另一个交点,点D与点C关于抛物线对称轴对称,作直线AD.点P在抛物线上,过点P作PE⊥x轴,垂足为点E,交直线AD于点Q,过点P作PG⊥AD,垂足为点G,连接AP.设点P的横坐标为m,PQ的长度为d.
(1)求抛物线的解析式;
(2)求点D的坐标及直线AD的解析式;
(3)当点P在直线AD上方时,求d关于m的函数关系式,并求出d的最大值;
(4)当点P在直线AD上方时,若PQ将△APG分成面积相等的两部分,直接写出m的值.
【答案】(1)y=﹣x2+2x+3;(2)点D的坐标为(2,3),直线AD的解析式为y=x+1;(3)d关于m函数关系式是d=﹣m2+m+2,d的最大值为![]() ;(4)m的值为0
;(4)m的值为0
【解析】
(1)根据待定系数法可求抛物线的解析式;
(2)将y=﹣x2+2x+3配方得抛物线的对称轴,根据轴对称的性质可得点D的坐标,再根据待定系数法可求直线AD的解析式;
(3)根据两点间的距离公式可得d=﹣m2+2m+3﹣m﹣1=﹣m2+m+2=﹣(m﹣![]() )2+
)2+![]() ,依此可求d的最大值;
,依此可求d的最大值;
(4)可设直线PG的解析式为y=﹣x+p,根据中点坐标公式可得G的坐标,再根据待定系数法可求m的值.
解:(1)∵抛物线y=﹣x2+bx+c 经过A(﹣1,0),C(0,3)两点,
∴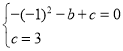 ,
,
解得![]() .
.
∴抛物线的解析式为y=﹣x2+2x+3.
(2)∵将y=﹣x2+2x+3配方,得y=﹣(x﹣1)2+4,
∴抛物线的对称轴是直线x=1.
∴点D的坐标为(2,3).
设直线AD的解析式为y=kx+n,
由题意,得![]() ,
,
解得![]() .
.
∴直线AD的解析式为y=x+1.
(3)∵点P的横坐标为m,
∴点P,Q的纵坐标分别为﹣m2+2m+3,m+1,
∴d=﹣m2+2m+3﹣m﹣1=﹣m2+m+2=![]() ,
,
∴d关于m函数关系式是d=﹣m2+m+2,d的最大值为![]() .
.
(4)设直线PG的解析式为y=﹣x+p,
∵PQ将△APG分成面积相等的两部分,
∴G的坐标为(2m+1,2m+2),
∴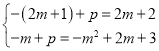 ,
,
解得m1=0,m2=﹣1(不合题意舍去).
故m的值为0.

 寒假学与练系列答案
寒假学与练系列答案