题目内容
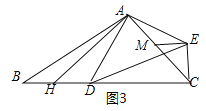
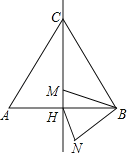
【题目】在△ABC中,∠ACB=45°,BC=5,AC=2![]() ,D是BC边上的动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接EC.
,D是BC边上的动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接EC.
(1)如图a,求证:CE⊥BC;
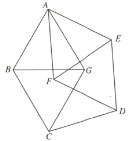
(2)连接ED,M为AC的中点,N为ED的中点,连接MN,如图b.
①写出DE、AC,MN三条线段的数量关系,并说明理由;
②在点D运动的过程中,当BD的长为何值时,M,E两点之间的距离最小?最小值是 ,请直接写出结果.
【答案】(1)见解析;(2)①MN2+![]() AC2=
AC2=![]() DE2,见解析;②当BD=2时,EM的值最小,1.
DE2,见解析;②当BD=2时,EM的值最小,1.
【解析】
(1)过点A作AH⊥AC交BC于H,如图1,易证△AHC是等腰直角三角形,由SAS可证△HAD≌△CAE,可得∠ACE=∠AHD=45°,即可证得结论;
(2)①连接AN,CN,由直角三角形的性质可得AN=CN=![]() DE,由等腰三角形的性质可得MN⊥AC,CM=
DE,由等腰三角形的性质可得MN⊥AC,CM=![]() AC,然后由勾股定理可得结论;
AC,然后由勾股定理可得结论;
②由(1)知∠ECB=90°,根据垂线段最短可知:当ME⊥EC时,ME的值最小,然后根据等腰直角三角形的判定和性质即可求出ME的长,再结合已知和(1)的结论依次求出HC、HD、CD的长,即可求得BD的长.
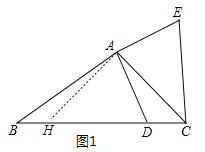
解:(1)证明:过点A作AH⊥AC交BC于H,如图1,
∵∠ACB=45°,AH⊥AC,
∴∠AHC=∠ACB=45°,
∴AH=AC,
∵将线段AD绕点A逆时针旋转90°得到线段AE,
∴AD=AE,∠HAC=∠DAE=90°,
∴∠HAD=∠CAE,
∴△HAD≌△CAE(SAS),
∴∠ACE=∠AHD=45°,
∴∠HCE=90°,
∴CE⊥BC;
(2)①MN2+![]() AC2=
AC2=![]() DE2.理由如下:连接AN,CN,如图2,
DE2.理由如下:连接AN,CN,如图2,
∵∠EAD=∠ECD=90°,点N是DE中点,
∴AN=CN=![]() DE,
DE,
∵M为AC的中点,
∴MN⊥AC,AM=CM=![]() AC,
AC,
∵MN2+CM2=CN2,
∴MN2+![]() AC2=
AC2=![]() DE2;
DE2;

②如图3中,由(1)可知∠ECB=90°,
∴CE⊥BC,
∴当ME⊥EC时,ME的值最小,
在Rt△AHC中,∵AH=AC=2![]() ,
,
∴HC=4,
∵M为AC中点,
∴AM=MC=![]() ,
,
在Rt△CME中,∵∠ECM=∠CME=45°,
∴EC=EM=1,
由(1)可知:△HAD≌△CAE,
∴HD=EC=1,
∴CD=4﹣1=3,
∴BD=5﹣3=2,
∴当BD=2时,EM的值最小,最小值为1,
故答案为:1.