题目内容
【题目】如图,二次函数![]() 图象的顶点为
图象的顶点为![]() ,其图象与
,其图象与![]() 轴的交点
轴的交点![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() ,
,![]() .与
.与![]() 轴负半轴交于点
轴负半轴交于点![]() ,在下面五个结论中:
,在下面五个结论中:
①![]() ;②
;②![]() ;③
;③![]() ;④只有当
;④只有当![]() 时,
时,![]() 是等腰直角三角形;⑤使
是等腰直角三角形;⑤使![]() 为等腰三角形的
为等腰三角形的![]() 值可以有四个.
值可以有四个.
其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
【答案】A
【解析】
先根据图象与x轴的交点A,B的横坐标分别为-1,3确定出AB的长及对称轴,再由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
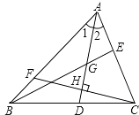
①∵图象与x轴的交点A,B的横坐标分别为-1,3,
∴AB=4,
∴对称轴x=-![]() =1,
=1,
即2a+b=0.
故①错误;
②根据图示知,当x=1时,y<0,即a+b+c<0.
故②错误;
③∵A点坐标为(-1,0),
∴a-b+c=0,而b=-2a,
∴a+2a+c=0,即c=-3a.
故③正确;
④当a=![]() ,则b=-1,c=-
,则b=-1,c=-![]() ,对称轴x=1与x轴的交点为E,如图,
,对称轴x=1与x轴的交点为E,如图,
∴抛物线的解析式为y=![]() x2-x-
x2-x-![]() ,
,
把x=1代入得y=![]() -1-
-1-![]() =-2,
=-2,
∴D点坐标为(1,-2),
∴AE=2,BE=2,DE=2,
∴△ADE和△BDE都为等腰直角三角形,
∴△ADB为等腰直角三角形.
故④正确;
⑤要使△ACB为等腰三角形,则必须保证AB=BC=4或AB=AC=4或AC=BC,
当AB=BC=4时,
∵AO=1,△BOC为直角三角形,
又∵OC的长即为|c|,
∴c2=16-9=7,
∵由抛物线与y轴的交点在y轴的负半轴上,
∴c=-![]() ,
,
与2a+b=0、a-b+c=0联立组成解方程组,解得a=![]() ;
;
同理当AB=AC=4时
∵AO=1,△AOC为直角三角形,
又∵OC的长即为|c|,
∴c2=16-1=15,
∵由抛物线与y轴的交点在y轴的负半轴上,
∴c=-![]()
与2a+b=0、a-b+c=0联立组成解方程组,解得a=![]() ;
;
同理当AC=BC时
在△AOC中,AC2=1+c2,
在△BOC中BC2=c2+9,
∵AC=BC,
∴1+c2=c2+9,此方程无解.
经解方程组可知只有两个a值满足条件.
故⑤错误.
综上所述,正确的结论是③④.
故选A.

【题目】现在要从甲、乙两名学生中选择一名学生去参加比赛,因甲乙两人的5次测试总成绩相同,所以根据他们的成绩绘制了尚不完整的统计图表进行分析.
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 90 | 70 | 80 | 100 | 60 |
乙成绩 | 70 | 90 | 90 | a | 70 |
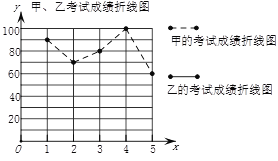
请同学们完成下列问题:
(1)a=________,![]() =________;
=________;
(2)请在图中完成表示乙成绩变化情况的折线:
(3)S2甲=200,请你计算乙的方差;
(4)可看出________将被选中参加比赛.(第1问和第4问答案可直接填写在答题卡的横线上)