ЬтФПФкШн
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНx2Љ2mx+m2Љ2гыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉХзЮяЯпЕФЖЅЕузјГЦЮЊЁЁ ЁЁЃЌЕуCзјБъЮЊЁЁ ЁЁЃЛЃЈгУКЌmЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ2ЃЉЕБmЃН1ЪБЃЌХзЮяЯпЩЯгавЛЖЏЕуPЃЌЩшPЕуКсзјБъЮЊnЃЌЧвnЃО0ЃЎ
ЂйШєЕуPЕНxжсЕФОрРыЮЊ2ЪБЃЌЧѓЕуPЕФзјБъЃЛ
ЂкЩшХзЮяЯпдкЕуCгыЕуPжЎМфВПЗжЃЈКЌЕуCКЭЕуPЃЉзюИпЕугызюЕЭЕузнзјБъжЎВюЮЊhЃЌЧѓhгыnжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПnЕФШЁжЕЗЖЮЇЃЛ
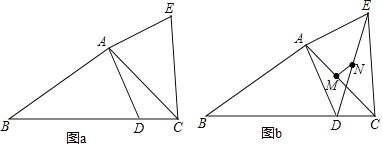
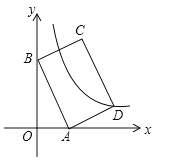
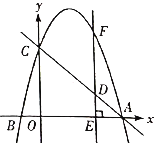
ЃЈ3ЃЉШєЕуAЃЈЉ3ЃЌ2ЃЉЁЂBЃЈ2ЃЌ2ЃЉЃЌСЌНсABЃЌЕБХзЮяЯпyЃНx2Љ2mx+m2Љ2гыЯпЖЮABжЛгавЛИіНЛЕуЪБЃЌжБНгаДГіmЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈmЃЌЉ2ЃЉЃЌЃЈ0ЃЌm2Љ2ЃЉЃЌЃЈ2ЃЉЂйP1ЃЈ1ЃЌЉ2ЃЉЃЌP2ЃЈ3ЃЌ2ЃЉЃЛЂк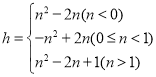 ЃЛЃЈ3ЃЉmЕФШЁжЕЗЖЮЇЮЊЉ5ЁмmЃМЉ1Лђ0ЃМmЁм4ЃЎ
ЃЛЃЈ3ЃЉmЕФШЁжЕЗЖЮЇЮЊЉ5ЁмmЃМЉ1Лђ0ЃМmЁм4ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЕБxЃН0ЪБЃЌЧѓГіyЕФжЕЃЌМДПЩаДГіЕуCзјБъЃЌНЋХзЮяЯпyЃНx2Љ2mx+m2Љ2ЛЏЮЊЖЅЕуЪНМДПЩаДГіЖЅЕузјБъЃЛ
ЃЈ2ЃЉЂйЕБmЃН1ЪБЃЌЯШЧѓГіХзЮяЯпЕФНтЮіЪНЃЌдйЗжБ№НЋyЃНЁР2ДњШыНтЮіЪНМДПЩЧѓГіЕуPзјБъЃЛ
ЂкгУКЌnЕФДњЪ§ЪНБэЪОГіЕуPЕФзјБъЃЌЗжЕуPдкyжсзѓВрЃЌдкyжсгвВрЧвдкЖдГЦжсзѓВрКЭгвВрШ§жжЧщПіЬжТлЃЌжБНгЧѓГізюИпЕугызюЕЭЕуЕФзнзјБъжЎВюМДПЩЃЛ
ЃЈ3ЃЉЗжСНжжЧщПіЬжТлЃЌЕБmЃМ0ЃЌХзЮяЯпОЙ§ЯпЖЮЕФзюзѓЖЫЕу![]() ЪБЃЌЧѓГіmЕФжЕВЂЛГіЭМЯѓМДПЩгЩЭМЯѓПДГіmЕФШЁжЕЗЖЮЇЃЛЕБmЁн0ЃЌХзЮяЯпОЙ§ЯпЖЮЕФзюгвЖЫЕуB
ЪБЃЌЧѓГіmЕФжЕВЂЛГіЭМЯѓМДПЩгЩЭМЯѓПДГіmЕФШЁжЕЗЖЮЇЃЛЕБmЁн0ЃЌХзЮяЯпОЙ§ЯпЖЮЕФзюгвЖЫЕуB![]() ЪБЃЌЧѓГіmЕФжЕВЂЛГіЭМЯѓМДПЩгЩЭМЯѓПДГіmЕФШЁжЕЗЖЮЇЃЎ
ЪБЃЌЧѓГіmЕФжЕВЂЛГіЭМЯѓМДПЩгЩЭМЯѓПДГіmЕФШЁжЕЗЖЮЇЃЎ
ЃЈ1ЃЉyЃНx2Љ2mx+m2Љ2
ЃНЃЈxЉmЃЉ2Љ2ЃЌ
ЁрЖЅЕузјБъЮЊЃЈmЃЌЉ2ЃЉЃЌ
дкyЃНx2Љ2mx+m2Љ2жаЃЌ
ЕБxЃН0ЪБЃЌyЃНm2Љ2ЃЌ
ЁрЕуCзјБъЮЊЃЈ0ЃЌm2Љ2ЃЉЃЌ
ЙЪД№АИЮЊЃКЃЈmЃЌЉ2ЃЉЃЌЃЈ0ЃЌm2Љ2ЃЉЃЛ
ЃЈ2ЃЉЂйЕБmЃН1ЪБЃЌyЃНx2Љ2xЉ1ЃЌ
ЁрPЃЈnЃЌn2Љ2nЉ2ЃЉЃЌ
Сюn2Љ2nЉ1ЃНЉ2ЃЌ
НтЕУЃЌn1ЃНn2ЃН1ЃЌ
ЁрP1ЃЈ1ЃЌЉ2ЃЉЃЛ
Сюn2Љ2nЉ1ЃН2ЃЌ
НтЕУЃЌn1ЃН3ЃЌn2ЃНЉ1ЃЈnЃО0ЃЌЩсШЅЃЉЃЌ
ЁрP2ЃЈ3ЃЌ2ЃЉЃЌ
злЩЯЃКP1ЃЈ1ЃЌЉ2ЃЉЃЌP2ЃЈ3ЃЌ2ЃЉЃЛ
ЂкдкyЃНx2Љ2xЉ1жаЃЌЖдГЦжсЮЊ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
ЁрЖЅЕузјБъЮЊ![]() ЃЌ
ЃЌ
ЁпЕуPЕФКсзјБъЮЊnЃЌ
ЁрЕуPЕФКсзјБъЮЊ![]() ЃЌ
ЃЌ
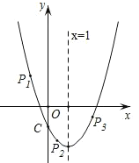
ШчЭМЃЌЕБЕуPдкyжсзѓВрЃЌМД![]() ЪБЃЌ
ЪБЃЌ
![]() ЃЛ
ЃЛ
ЕБдкyжсгвВрЧвдкЖдГЦжсзѓВрЃЌМД![]() ЪБЃЌ
ЪБЃЌ
![]() ЃЛ
ЃЛ
ЕБдкЖдГЦжсгвВрЃЌМД![]() ЪБЃЌ
ЪБЃЌ
![]() ЃЛ
ЃЛ
злЩЯЃК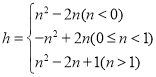
ЃЈ3ЃЉЂйЕБmЃМ0ЃЌХзЮяЯпОЙ§ЯпЖЮЕФзюзѓЖЫЕуAЃЈЉ3ЃЌ2ЃЉЪБЃЌ
ЃЈЉ3ЉmЃЉ2Љ2ЃН2ЃЌ
НтЕУЃЌm1ЃНЉ5ЃЌm2ЃНЉ1ЃЌ
ЁрЖдгІХзЮяЯпЕФЭМЯѓШчЭМ1ЃЌЭМ2ЫљЪОЃЌ

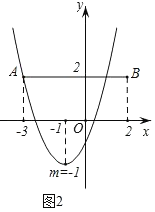
гЩЭМЯѓПЩвдПДГіЕБЉ5ЁмmЃМЉ1ЪБЃЌХзЮяЯпyЃНx2Љ2mx+m2Љ2гыЯпЖЮABжЛгавЛИіНЛЕуЃЛ
ЂкЕБmЁн0ЃЌХзЮяЯпОЙ§ЯпЖЮЕФзюгвЖЫЕуBЃЈ2ЃЌ2ЃЉЪБЃЌ
ЃЈ2ЉmЃЉ2Љ2ЃН2ЃЌ
НтЕУЃЌm1ЃН4ЃЌm2ЃН0ЃЌ
ЁрЖдгІХзЮяЯпЕФЭМЯѓШчЭМ3ЃЌЭМ4ЫљЪОЃЌ

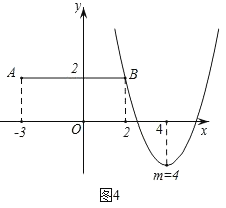
гЩЭМЯѓПЩвдПДГіЕБ0ЃМmЁм4ЪБЃЌХзЮяЯпyЃНx2Љ2mx+m2Љ2гыЯпЖЮABжЛгавЛИіНЛЕуЃЛ
злЩЯЫљЪіЃКmЕФШЁжЕЗЖЮЇЮЊЉ5ЁмmЃМЉ1Лђ0ЃМmЁм4ЃЎ

 ЭЌВНСЗЯАЧПЛЏЭиеЙЯЕСаД№АИ
ЭЌВНСЗЯАЧПЛЏЭиеЙЯЕСаД№АИЁОЬтФПЁПвбжЊвЛИіЖўДЮКЏЪ§ЭМЯѓЩЯВПЗжЕуЕФКсзјБъ![]() гызнзјБъ
гызнзјБъ![]() ЕФЖдгІжЕШчЯТБэЫљЪОЃК
ЕФЖдгІжЕШчЯТБэЫљЪОЃК
| ... |
|
|
|
|
| ... |
| ... |
|
|
|
|
| ... |
ЃЈ1ЃЉЧѓетИіЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉдкИјЖЈЕФЦНУцжБНЧзјБъЯЕжаЛГіетИіЖўДЮКЏЪ§ЕФЭМЯѓЃЛ
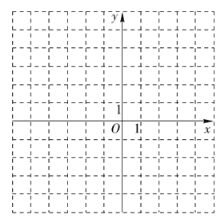
ЃЈ3![]() ЪБЃЌ
ЪБЃЌ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ