Question

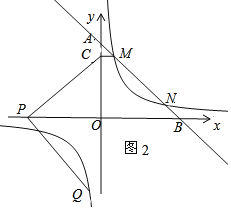
【题目】如图，一次函数y＝﹣x+5的图象与坐标轴交于A，B两点，与反比例函数y＝的图象交于M，N两点，过点M作MC⊥y轴于点C，且CM＝1，过点N作ND⊥x轴于点D，且DN＝1．已知点P是x轴（除原点O外）上一点．

（1）直接写出M、N的坐标及k的值；

（2）将线段CP绕点P按顺时针或逆时针旋转90°得到线段PQ，当点P滑动时，点Q能否在反比例函数的图象上？如果能，求出所有的点Q的坐标；如果不能，请说明理由；

（3）当点P滑动时，是否存在反比例函数图象（第一象限的一支）上的点S，使得以P、S、M、N四个点为顶点的四边形是平行四边形？若存在，请直接写出符合题意的点S的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）M（1，4），N（4，1），k＝4；（2）（2+2，﹣2+2）或（2﹣2，﹣2﹣2）或（﹣2，﹣2）；（3）（，5）或（，3）．

【解析】

（1）利用待定系数法即可解决问题；

（2）分三种情形求解：①如图2，点P在x轴的正半轴上时，绕P顺时针旋转到点Q，根据△COP≌△PHQ，得CO＝PH，OP＝QH，设P（x，0），表示Q（x+4，x），代入反比例函数的关系式中可得Q的两个坐标；②如图3，点P在x轴的负半轴上时；③如图4，点P在x轴的正半轴上时，绕P逆时针旋转到点Q，同理可得结论．

（3）分两种情形分别求解即可；

解：（1）由题意M（1，4），n（4，1），

∵点M在y＝上，

∴k＝4；

（2）当点P滑动时，点Q能在反比例函数的图象上；

如图1，CP＝PQ，∠CPQ＝90°，

过Q作QH⊥x轴于H，

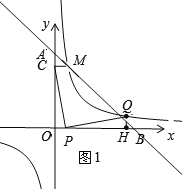
易得：△COP≌△PHQ，

∴CO＝PH，OP＝QH，

由（2）知：反比例函数的解析式：y＝；

当x＝1时，y＝4，

∴M（1，4），

∴OC＝PH＝4

设P（x，0），

∴Q（x+4，x），

当点Q落在反比例函数的图象上时，

x（x+4）＝4，

x2+4x+4＝8，

x＝﹣2±，

当x＝﹣2±时，x+4＝2+，如图1，Q（2+2，2+2）；

当x＝﹣2﹣2时，x+4＝2﹣2，如图2，Q（2﹣2，2﹣2）；

如图3，CP＝PQ，∠CPQ＝90°，设P（x，0）

过P作GH∥y轴，过C作CG⊥GH，过Q作QH⊥GH，

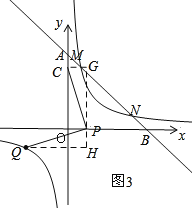
易得：△CPG≌△PQH，

∴PG＝QH＝4，CG＝PH＝x，

∴Q（x﹣4，﹣x），

同理得：﹣x（x﹣4）＝4，

解得：x1＝x2＝2，

∴Q（﹣2，﹣2），

综上所述，点Q的坐标为（2+2，﹣2+2）或（2﹣2，﹣2﹣2）或（﹣2，﹣2）．

（3）当MN为平行四边形的对角线时，根据MN的中点的纵坐标为，可得点S的纵坐标为5，即S（，5）；

当MN为平行四边形的边时，易知点S的纵坐标为3，即S（，3）；

综上所述，满足条件的点S的坐标为（，5）或（，3）．