Question

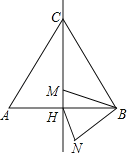
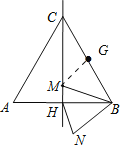
【题目】如图，边长为5的等边三角形ABC中，M是高CH所在直线上的一个动点，连接MB，将线段BM绕点B逆时针旋转60°得到BN，连接HN．则在点M运动过程中，线段HN长度的最小值是_____．

Answer 1

【答案】1.25

【解析】

取CB的中点G，连接MG，如图，根据等边三角形的性质和旋转的性质可得：∠HBN＝∠GBM，HB＝BG，MB＝NB，然后利用SAS即可证明△MBG≌△NBH，进而可得HN＝MG，然后根据垂线段最短可得MG⊥CH时，MG最短，再根据∠BCH＝30°求解即可．

解：如图，取BC的中点G，连接MG，

∵旋转角为60°，∴∠MBH+∠HBN＝60°，

∵△ABC是等边三角形，∴∠MBH+∠MBC＝∠ABC＝60°，∴∠HBN＝∠GBM，

∵CH是等边△ABC的对称轴，∴HB＝AB，∴HB＝BG，

又∵MB旋转到BN，∴BM＝BN，

∴△MBG≌△NBH（SAS），∴MG＝NH，

根据垂线段最短可知：当MG⊥CH时，MG最短，即HN最短，

此时∵∠BCH＝×60°＝30°，CG＝AB＝×5＝2.5，

∴MG＝CG＝×2.5＝1.25，∴HN＝1.25，

故答案为：1.25．