题目内容
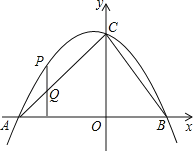
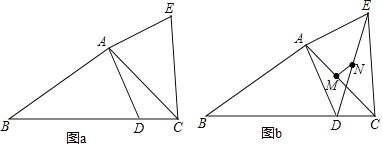
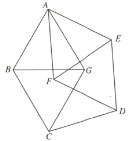
【题目】如图所示,平面上七个点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,图中所有的连线长均相等,则
,图中所有的连线长均相等,则![]() ______.
______.
【答案】![]()
【解析】
连接AC、AD,由各边都相等,得△ABG、△AEF、△CBG和△DEF都是等边三角形,四边形ABCG、四边形AEDF是菱形,若设AB的长为x,根据等边三角形、菱形的性质,计算出AD的长![]() ,∠BAC=∠EAD=30°,证明∠BAF=∠CAD,在△CAD中构造直角△AMD,利用勾股定理求出cos∠CAD.
,∠BAC=∠EAD=30°,证明∠BAF=∠CAD,在△CAD中构造直角△AMD,利用勾股定理求出cos∠CAD.
连接AC、AD,过点D作DM⊥AC,垂直为M.

设AE的长为x,则AB=AG=BG=CG=CB=AF=AE=EF=x,
∴△ABG、△AEF、△CBG和△DEF都是等边三角形,四边形ABCG、四边形AEDF是菱形,
∴∠BAC=∠EAD=30°
∴![]()
∵∠CAD=∠BAE-∠BAC-∠EAD=∠BAE-60°,
∠BAF=∠BAE-∠EAF=∠BAE-60°
∴∠BAF=∠CAD
在Rt△AMD中,因为DM=![]()
AM=cos∠CAD![]() ,CM=
,CM=![]()
在Rt△CMD中,CD2=CM2+MD2,
即![]()
整理,得![]()
∴cos∠CAD=![]()
∴cos∠BAF=![]()
故答案为:![]() .
.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中,m= .
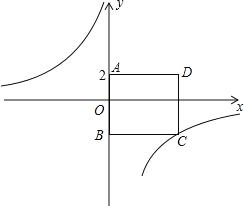
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=2有 个实数根.

③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 .
【题目】运动员将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间t(s)满足二次函数关系,t与h的几组对应值如下表所示.
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度;
(3)问:小球的飞行高度能否达到22m?请说明理由.