题目内容
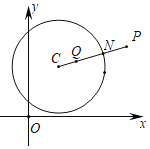
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:连接PC交⊙C于点N,若点P关于点N的对称点Q在⊙C的内部,则称点P是⊙C的外称点.
(1)当⊙O的半径为1时,
①在点D(﹣1,﹣1),E(2,0),F(0,4)中,⊙O的外称点是 ;
②若点M(m,n)为⊙O的外称点,且线段MO交⊙O于点G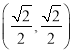 ,求m的取值范围;
,求m的取值范围;
(2)直线y=﹣x+b过点A(1,1),与x轴交于点B.⊙T的圆心为T(t,0),半径为1.若线段AB上的所有点都是⊙T的外称点,请直接写出t的取值范围.
【答案】(1)①D,E;②![]() <m<
<m<![]() ;(2)﹣1<t<2﹣
;(2)﹣1<t<2﹣![]() 或3<t<1+2
或3<t<1+2![]() .
.
【解析】
(1)①根据⊙O的外应点的定义,画出图形即可判断;
②作射线GO,交⊙O于点H(﹣![]() ,﹣
,﹣![]() ),作点H关于点G的对称点H'(
),作点H关于点G的对称点H'(![]() ,
,![]() ),由点M为⊙O的外应点,推出点M在线段GH'上(不与G,H'重合),由此即可解决问题;
),由点M为⊙O的外应点,推出点M在线段GH'上(不与G,H'重合),由此即可解决问题;
(2)求出四种特殊位置t的值即可判断.
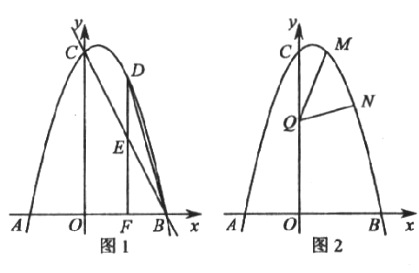
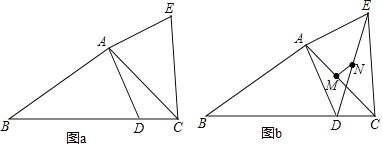
(1)①如图1中,
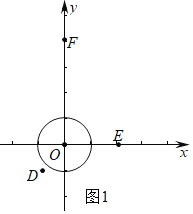
根据点P是⊙O的外应点定义,观察图象可知,⊙O的外应点是D,E.
故答案为D,E.
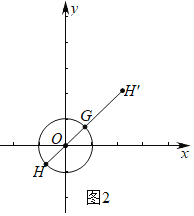
②如图2中,作射线GO,交⊙O于点H(﹣![]() ,﹣
,﹣![]() ),
),
作点H关于点G的对称点H'(![]() ,
,![]() ),
),
∵点M为⊙O的外应点,
∴点M在线段GH'上(不与G,H'重合).
∴![]() <m<
<m<![]() .
.
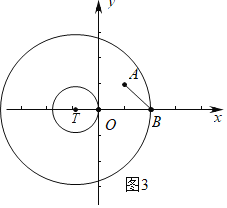
(2)由题意A(1,1),∵直线y=﹣x+b过点A(1,1),
∴b=2,可得B(2,0)
如图3中,当半径为3的⊙T经过点B时,T(﹣1,0)
如图4中,当半径为1的⊙T与AB相切于F时,易知TF=FB=1,TB=![]() ,
,
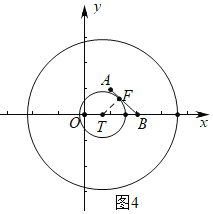
∴OT=2﹣![]() ,
,
∴T(2﹣![]() ,0)
,0)
观察图象可知:当﹣1<t<2﹣![]() 时,线段AB上的所有点都是⊙T的外应点;
时,线段AB上的所有点都是⊙T的外应点;
如图5中,当半径为1的⊙T经过点B时,T(3,0),
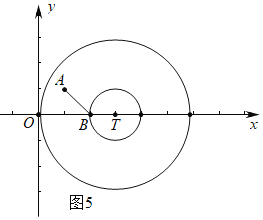
如图6中,当半径为3的⊙T经过点A时,易知T(1+2![]() ,0)
,0)
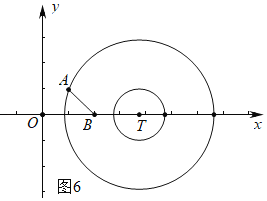
观察图象可知:当3<t<1+2![]() 时,线段AB上的所有点都是⊙T的外应点,
时,线段AB上的所有点都是⊙T的外应点,
综上所述,满足条件的t的值为:﹣1<t<2﹣![]() 或3<t<1+2
或3<t<1+2![]() .
.

 阅读快车系列答案
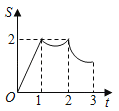
阅读快车系列答案【题目】运动员将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间t(s)满足二次函数关系,t与h的几组对应值如下表所示.
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度;
(3)问:小球的飞行高度能否达到22m?请说明理由.

【题目】已知一个二次函数图象上部分点的横坐标![]() 与纵坐标
与纵坐标![]() 的对应值如下表所示:
的对应值如下表所示:
| ... |
|
|
|
|
| ... |
| ... |
|
|
|
|
| ... |
(1)求这个二次函数的表达式;
(2)在给定的平面直角坐标系中画出这个二次函数的图象;
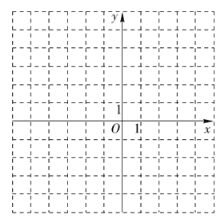
(3![]() 时,
时,![]() 的取值范围.
的取值范围.