题目内容
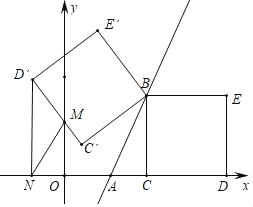
【题目】如图,在⊙O中,直径AB=8,∠A=30°,AC=8![]() ,AC与⊙O交于点D.
,AC与⊙O交于点D.
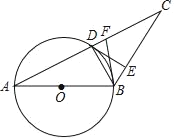
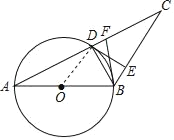
(1)求证:直线BD是线段AC的垂直平分线;
(2)若过点D作DE⊥BC,垂足为E,求证:DE是⊙O的切线;
(3)若点F是AC的三等分点,求BF的长.
【答案】(1)见解析;(2)见解析;(3)BF=![]() .
.
【解析】
(1)根据圆周角定理得到∠ADB=90°,解直角三角形得到BD=4,AD=4![]() ,于是得到AD=
,于是得到AD=![]() AC,即可得到结论;
AC,即可得到结论;
(2)连接OD,根据三角形中位线的性质得到OD∥BC,OD=![]() BC,推出OD⊥DE,于是得到DE是⊙O的切线;
BC,推出OD⊥DE,于是得到DE是⊙O的切线;
(3)根据已知条件得到AF=![]() ,求得DF=
,求得DF=![]() ,根据勾股定理即可得到结论.
,根据勾股定理即可得到结论.
∵(1)∵AB是⊙O的直径,
∴∠ADB=90°,
∵直径AB=8,∠A=30°,
∴BD=4,AD=4![]() ,
,
∵AC=8![]() ,
,
∴AD=![]() AC,
AC,
∴直线BD是线段AC的垂直平分线;
(2)连接OD,
∵D,O分别是线段AC,AB的中点,
∴OD∥BC,OD=![]() BC,
BC,
∵DE⊥BC,
∴∠DEC=∠EDO=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(3)∵点F是AC的三等分点,
∴AF=![]() ,
,
∵AD=4![]() ,
,
∴DF=![]() ,
,
∵BD⊥AC,BD=4,
∴BF=![]() .
.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
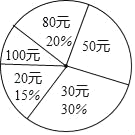
【题目】在“全民读书月”活动中,小明调查了班级里40名同学本学期购买课外书的费用情况,并将结果绘制成如图所示的统计表和扇形统计图,请根据相关信息,解答下列问题:(直接填写结果)
费用(元) | 20 | 30 | 50 | 80 | 100 |
人数 | 6 | a | 10 | b | 4 |
(1)本次调查获取的样本数据的众数是 元,中位数是 元;
(2)扇形统计图中,“50元”所对应的圆心角的度数为 度,该班学生购买课外书的平均费用为 元;
(3)若该校共有学生1000人,根据样本数据,估计本学期购买课外书花费50元的学生有 人.