题目内容
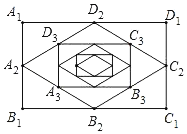
【题目】如图:顺次连接矩形A1B1C1D1四边的中点得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点得四边形A3B3C3D3,…,按此规律得到四边形AnBnnDn.若矩形A1B1C1D1的面积为8,那么四边形AnBnnDn的面积为_____.
【答案】24-n
【解析】
根据矩形A1B1C1D1面积、四边形A2B2C2D2的面积、四边形A3B3C3D3的面积,即可发现新四边形与原四边形的面积的一半,找到规律即可解题.
解:顺次连接矩形A1B1C1D1四边的中点得到四边形A2B2C2D2,则四边形A2B2C2D2的面积为矩形A1B1C1D1面积的一半,
顺次连接四边形A2B2C2D2四边的中点得四边形A3B3C3D3,则四边形A3B3C3D3的面积为四边形A2B2C2D2面积的一半,
故新四边形与原四边形的面积的一半,
则四边形AnBnCnDn面积为矩形A1B1C1D1面积的![]() ,
,
∴四边形AnBnCnDn面积=![]() ×8=24-n.
×8=24-n.
故答案为:24-n.

练习册系列答案
相关题目