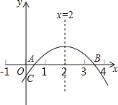题目内容
【题目】如图,在平面直角坐标系中,点A的坐标为(0,1),点B是x轴正半轴上一点,以AB为边作等腰直角三角形ABC,使∠BAC=90°,点C在第一象限,若点C在函数y=![]() (x>0)的图象上,则△ABC的面积为( )
(x>0)的图象上,则△ABC的面积为( )
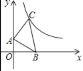
A. 1B. 2C. ![]() D. 3.
D. 3.
【答案】C
【解析】
过点C作![]() 轴,可证
轴,可证![]() ≌
≌![]() ,可得
,可得![]() ,即可求OM的长,由勾股定理可求AC的长,即可求
,即可求OM的长,由勾股定理可求AC的长,即可求![]() 的面积.
的面积.
解:如图,过点C作CM⊥y轴,
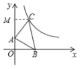
∵点A的坐标为(0,1),
∴OA=1
∵△ABC是等腰直角三角形
∴AC=AB,∠BAC=90°
∴∠CAM+∠OAB=90°,且∠OAB+∠ABO=90°
∴∠CAM=∠ABO,且AC=AB,∠CMA=∠AOB=90°
∴△AOB≌△CMA(AAS)
∴MC=AO=1
∴点C的横坐标为1,
∵若点C在函数![]() (x>0)的图象上,
(x>0)的图象上,
∴当x=1时,y=3
∴OM=3,
∴AM=OM﹣OA=2
∴AC=![]()
![]()
故选:C.

【题目】随着生活水平的提高,人们对空气质量的要求也越来越高,为了了解3月中旬长春市城区的空气质量情况,某校“综合实践环境调查小组”,从“2345天气预报”网,抽取了朝阳区和南关区这两个城区2019年3月11日﹣2019年3月20日的空气质量指数,作为样本进行统计,过程如下,请补充完整收集数据
朝阳区 | 167 | 61 | 79 | 78 | 97 | 153 | 59 | 179 | 85 | 209 |
南关区 | 74 | 54 | 47 | 47 | 43 | 43 | 59 | 104 | 119 | 251 |
(备注:空气质量指数,简称AQI,是定期描述空气质量的)
整理、描述数据按下表整理,描述这两城区空气质量指数的数据:
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 |
朝阳区 |
|
|
|
|
|
南关区 | 4 | 3 | 2 | 0 | 1 |
(说明:空气质量指数≤50时,空气质量为优,50<空气质量指数≤100时,空气场量为良,100<空气质量指数≤150时,空气质量为轻微污染,150<空气质量指数≤200时,空气质量为中度污染,200<空气质量指数≤300时,空气质量为重度污染)
分析数据
两城区的空气质量指数的平均数、中位数、方差如下表所示
城区 | 平均数 | 中位数 | 方差 |
朝阳区 | 116.7 | 91 | 2999.12 |
南关区 | 84.1 |
| 4137.66 |
请将以上两个表格补充完整得出结论
可以推断出哪个城区这十天中空气质量情况比较好?请至少从两个不同的角度说明推断的合理性