ћвƒњƒЏ»Ё
°Њћвƒњ°њќнц≤ «ґ‘іу∆ш÷–Єч÷÷–ьЄ°њ≈Ѕ£ќпЇђЅњ≥ђ±кµƒЅэЌ≥±н ц£ђќнц≤µƒ÷ч“™ќ£Ї¶њ…єйƒ…ќ™Ѕљ÷÷£Ї“ї «ґ‘»Ћће≤ъ…ъќ£Ї¶£ђґю «ґ‘љїЌ®≤ъ…ъќ£Ї¶£Ѓќнц≤ћм∆ш «“ї÷÷іу∆шќџ»Њ„іћђ£ђ≥…ґЉ –«шґђћмќнц≤ћм∆ш±»љѕ—ѕ÷Ў£ђЇ№ґаЉ“Ќ•–Ћ∆рЅЋќ™Љ“јпћн÷√°∞њ’∆ш«еља∆ч°±µƒ»»≥±£ђќ™іЋ£ђќ“ –ƒ≥…ћ≥°ЄщЊЁ√с÷Џљ°њµ“™£ђіъјнѕъ џƒ≥÷÷љшЉџќ™600‘™/ћ®µƒЉ“”√°∞њ’∆ш«еља∆ч°±£ЃЊ≠єэ –≥°ѕъ џЇуЈҐѕ÷£Ї‘Џ“їЄц‘¬ƒЏ£ђµ± џЉџ «700‘™/ћ® ±£ђњ… џ≥ц350ћ®£ђ«“ џЉџ√њћбЄя10‘™£ђЊЌїб…ў џ≥ц5ћ®£Ѓ
£®1£© ‘»Јґ®‘¬ѕъ џЅњy£®ћ®£©”л џЉџx£®‘™/ћ®£©÷ЃЉдµƒЇѓ эєЎѕµ љ£ї
£®2£©«лЉ∆Ћгµ± џЉџx£®‘™ћ®£©ґ®ќ™ґа…ў ±£ђЄ√…ћ≥°√њ‘¬ѕъ џ’в÷÷°∞њ’∆ш«еља∆ч°±Ћщїсµ√µƒјы»уW£®‘™£©„оіу£њ„оіујы»у «ґа…ў£њ
£®3£©»ф’юЄЃЉ∆їЃеа—°≤њЈ÷…ћ≥°£ђљЂѕъ џ°∞њ’∆ш«еља∆ч°±ƒ…»л√с…ъє§≥ћѕоƒњ£ђєжґ®£Ї√њѕъ џ“їћ®°∞њ’∆шЬ[ља∆ч°±£ђ≤∆’ю≤єћщ…ћЉ“200‘™£ђµЂѕъ џјы»у≤їƒ№Єя”ЏљшЉџµƒ25%£ђ«лќ £ЇЄ√…ћ≥°ѕлїс»°„оіујы»у£ђ «Јс≤ќ”лЊЇ±кіЋ√с…ъє§≥ћѕоƒњ£њ≤ҐЋµ√чјн”…£Ѓ
°Њір∞Є°њ£®1£©![]() £ї£®2£©µ±x£љ100 ±£ђw£љ80000£ї£®3£©Є√…ћ≥°ѕлїс»°„оіујы»у£ђїб≤ќ”лЊЇ±кіЋ√с…ъє§≥ћѕоƒњ£Ѓ
£ї£®2£©µ±x£љ100 ±£ђw£љ80000£ї£®3£©Є√…ћ≥°ѕлїс»°„оіујы»у£ђїб≤ќ”лЊЇ±кіЋ√с…ъє§≥ћѕоƒњ£Ѓ
°Њљвќц°њ
£®1£©”…ћв“вµ√£Їy£љ350©Б![]() £®x©Б700£©£ђЉіњ…«уљв£ї
£®x©Б700£©£ђЉіњ…«уљв£ї
£®2£©”…ћв“вµ√£Їw£љy£®x©Б600£©£ђЉіњ…«уљв£ї
£®3£©√њћ®ѕъ џјы»у≤їƒ№Єя”ЏљшЉџµƒ25%£ђЉі600°Ѕ£®1+25%£©£љ750£ђЉі£Їx°№750£ђ”…ћв“вµ√£Їw£љ£®700©Б![]() x£©£®x©Б600+200£©£љ©Б
x£©£®x©Б600+200£©£љ©Б![]() £®x©Б1400£©£®x©Б400£©£ђx°№750 ±£ђµ±x£љ750 ±£ђ»°µ√„оіу÷µјы»у£ђЉіњ…«уљв£Ѓ
£®x©Б1400£©£®x©Б400£©£ђx°№750 ±£ђµ±x£љ750 ±£ђ»°µ√„оіу÷µјы»у£ђЉіњ…«уљв£Ѓ
£®1£©”…ћв“вµ√£Їy£љ350©Б![]() £®x©Б700£©£љ©Б
£®x©Б700£©£љ©Б![]() x+700£ї
x+700£ї
£®2£©”…ћв“вµ√£Їw£љy£®x©Б600£©£љ©Б![]() £®x©Б600£©£®x©Б1400£©£ђ
£®x©Б600£©£®x©Б1400£©£ђ
°я-![]() £Љ0£ђє Їѓ э”–„оіу÷µ£ђµ±x£љ©Б
£Љ0£ђє Їѓ э”–„оіу÷µ£ђµ±x£љ©Б![]() £љ100 ±£ђw£љ80000£ї
£љ100 ±£ђw£љ80000£ї
£®3£©√њћ®ѕъ џјы»у≤їƒ№Єя”ЏљшЉџµƒ25%£ђЉі600°Ѕ£®1+25%£©£љ750£ђЉі£Їx°№750£ђ
”…ћв“вµ√£Їw£љ£®700©Б![]() x£©£®x©Б600+200£©£љ©Б
x£©£®x©Б600+200£©£љ©Б![]() £®x©Б1400£©£®x©Б400£©£ђ
£®x©Б1400£©£®x©Б400£©£ђ
x°№750 ±£ђµ±x£љ750 ±£ђ»°µ√„оіу÷µјы»уќ™£Ї113750£Њ80000£ђ
є £ЇЄ√…ћ≥°ѕлїс»°„оіујы»у£ђїб≤ќ”лЊЇ±кіЋ√с…ъє§≥ћѕоƒњ£Ѓ

°Њћвƒњ°њќ™≈дЇѕ»Ђ –°∞љы÷єЈў…’љ’Є—°±є§„ч£ђƒ≥—І–£Њў––ЅЋ°∞љы÷єЈў…’љ’Є—£ђ±£ї§їЈЊ≥£ђі”ќ“„ц∆р°±ќ™÷чћвµƒ—Ёљ≤±»»ь. »ьЇу„йќѓїб’ыјн≤ќ»ьЌђ—Іµƒ≥…Љ®£ђ≤Ґ÷∆„чЅЋ»зѕ¬≤їЌк’ыµƒ∆µ эЈ÷≤Љ±нЇЌ∆µ эЈ÷≤Љ÷±ЈљЌЉ£ђ«лЄщЊЁЌЉ±нћбє©µƒ–≈ѕҐ£ђљвірѕ¬Ѕ–ќ ћв£Ї
Ј÷ эґќ £®Ј÷ эќ™xЈ÷£© | ∆µ э | ∞ўЈ÷±» |
60°№x£Љ70 | 8 | 20% |
70°№x£Љ80 | a | 30% |
80°№x£Љ90 | 16 | b% |
90°№x£Љ100 | 4 | 10% |
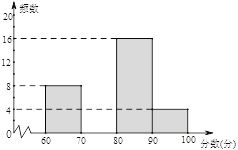
£®1£©±н÷–µƒa£љ £ђb£љ°°°°°°°°°°£ї
£®2£©«л≤є»Ђ∆µ эЈ÷≤Љ÷±ЈљЌЉ£ї
£®3£©»ф”√…»–ќЌ≥Љ∆ЌЉјі√и ц≥…Љ®Ј÷≤Љ«йњц£ђ‘тЈ÷ эґќ70°№x£Љ80ґ‘”¶µƒ‘≤–ƒљ«µƒґ» э « £ї
£®4£©ЊЇ»ь≥…Љ®≤їµЌ”Џ90Ј÷µƒ4√ыЌђ—І÷–’эЇ√”–2√ыƒ–Ќђ—І£ђ2√ы≈ЃЌђ—І.—І–£і”’в4√ыЌђ—І÷–Ћжїъ≥й»°2√ыЌђ—Іљ” №µз ”ћ®Љ«’я≤…Ј√£ђ«л”√Ѕ–±нїтї≠ ч„іЌЉµƒЈљЈ®«у’эЇ√≥йµљ“ї√ыƒ–Ќђ—ІЇЌ“ї√ы≈ЃЌђ—ІµƒЄ≈¬ .