题目内容
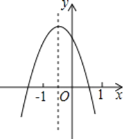
【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图，分析下列四个结论：①abc＜0；②b2-4ac＞0；③a+b+c＞0；④a-b+c＞0．其中正确的结论有（ ）
A. 1个
B. 2个
C. 3个
D. 4个
【答案】B
【解析】
①由抛物线的开口方向，抛物线与y轴交点的位置、对称轴即可确定a、b、c的符号，即得abc的符号；
②由抛物线与x轴有两个交点判断即可；
③x＝1时，y＜0，即a+b＋c＜0；
④x＝1时，y＞0，即ab＋c＞0．
解：①由抛物线开口向下，可得a＜0，又由抛物线与y轴交于正半轴，可得c＞0，然后由对称轴在y轴左侧，得到b与a同号，则可得b＜0，abc＞0，故①错误；
②由抛物线与x轴有两个交点，可得b24ac＞0，故②正确；
③x＝1时，y＜0，即a+b＋c＜0，故③错误；
④x＝1时，y＞0，即ab＋c＞0，故④正确．
综上所述，正确的结论有2个．
故选：B．
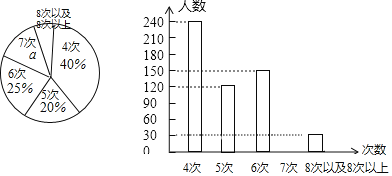
【题目】随着生活水平的提高，人们对空气质量的要求也越来越高，为了了解3月中旬长春市城区的空气质量情况，某校“综合实践环境调查小组”，从“2345天气预报”网，抽取了朝阳区和南关区这两个城区2019年3月11日﹣2019年3月20日的空气质量指数，作为样本进行统计，过程如下，请补充完整收集数据
朝阳区 | 167 | 61 | 79 | 78 | 97 | 153 | 59 | 179 | 85 | 209 |
南关区 | 74 | 54 | 47 | 47 | 43 | 43 | 59 | 104 | 119 | 251 |
（备注：空气质量指数，简称AQI，是定期描述空气质量的）
整理、描述数据按下表整理，描述这两城区空气质量指数的数据：
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 |
朝阳区 |
|
|
|
|
|
南关区 | 4 | 3 | 2 | 0 | 1 |
（说明：空气质量指数≤50时，空气质量为优，50＜空气质量指数≤100时，空气场量为良，100＜空气质量指数≤150时，空气质量为轻微污染，150＜空气质量指数≤200时，空气质量为中度污染，200＜空气质量指数≤300时，空气质量为重度污染）
分析数据
两城区的空气质量指数的平均数、中位数、方差如下表所示
城区 | 平均数 | 中位数 | 方差 |
朝阳区 | 116.7 | 91 | 2999.12 |
南关区 | 84.1 |
| 4137.66 |
请将以上两个表格补充完整得出结论
可以推断出哪个城区这十天中空气质量情况比较好？请至少从两个不同的角度说明推断的合理性
