Question

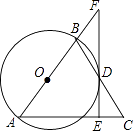
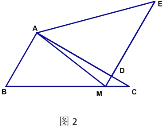
【题目】如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，AF平分∠CAB，交CD于点E，交CB于点F．若AC=3，AB=5，则CE的长为（　　）

A. B. C. D.

Answer 1

【答案】A

【解析】

根据三角形的内角和定理得出∠CAF+∠CFA=90°，∠FAD+∠AED=90°，根据角平分线和对顶角相等得出∠CEF=∠CFE，即可得出EC=FC，再利用相似三角形的判定与性质得出答案．

过点F作FG⊥AB于点G，

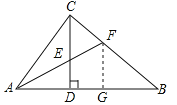
∵∠ACB=90°，CD⊥AB，∴∠CDA=90°，∴∠CAF+∠CFA=90°，∠FAD+∠AED=90°，∵AF平分∠CAB，∴∠CAF=∠FAD，∴∠CFA=∠AED=∠CEF，∴CE=CF，∵AF平分∠CAB，∠ACF=∠AGF=90°，∴FC=FG，∵∠B=∠B，∠FGB=∠ACB=90°，∴△BFG∽△BAC，∴，∵AC=3，AB=5，∠ACB=90°，∴BC=4，∴，∵FC=FG，∴，解得：FC=，即CE的长为．故选A．