题目内容
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于E交AB的延长线于点F.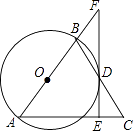
(1)求证:EF是⊙O的切线;
(2)若AE=6,FB=4,求⊙O的面积.
【答案】
(1)证明:连结AD、OD,如图,
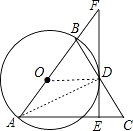
∵AB为⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD,
而OA=OB,
∴OD为△ABC的中位线,
∴OD∥AC,
∵EF⊥AC,
∴OD⊥EF,
∴EF是⊙O的切线
(2)解:设⊙O的半径为R,
∵OD∥AE,
∴△FOD∽△FAE,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得R=4,
∴⊙O的面积=π42=16π.
【解析】(1)连结AD、OD,根据圆周角定理可得到∠ADB=90°,即AD⊥BC,再根据等腰三角形的性质得BD=CD,则OD为△ABC的中位线,依据三角形的中位线定理可得到OD∥AC,加上EF⊥AC,于是OD⊥EF,最后,根据切线的判定定理进行证明即可;
(2)设⊙O的半径为R,利用OD∥AE得到△FOD∽△FAE,然后依据相似三角形对应边成比例可得到关于R的方程,从而可求得R的值,然后利用圆的面积公式求解即可.
【考点精析】认真审题,首先需要了解圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半),还要掌握切线的判定定理(切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线)的相关知识才是答题的关键.

 初中暑期衔接系列答案
初中暑期衔接系列答案【题目】列方程解应用题
某中学七年级![]() 两个班共105人,要去市科技博物馆进行社会大课堂活动,老师指派小明到网上查阅票价信息,小明查得票价如下表:其中七
两个班共105人,要去市科技博物馆进行社会大课堂活动,老师指派小明到网上查阅票价信息,小明查得票价如下表:其中七![]() 班不足50人,经估算,如果两个班都以班为单位购票,一共应付1140元.
班不足50人,经估算,如果两个班都以班为单位购票,一共应付1140元.
购票张数 | 每张票的价格 |
| 12 |
| 10 |
100以上 | a |
(1)两个班各有多少学生?
(2)如果两个班联合起来,作为一个团体购票,可以省300元,请求a的值.