题目内容
【题目】如图.AB是⊙O的直径,E为弦AP上一点,过点E作EC⊥AB于点C,延长CE至点F,连接FP,使∠FPE=∠FEP,CF交⊙O于点D. 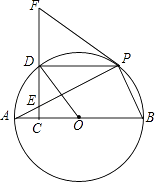
(1)证明:FP是⊙O的切线;
(2)若四边形OBPD是菱形,证明:FD=ED.
【答案】
(1)证明:连接OP,
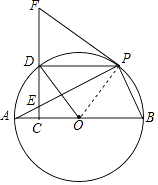
∵OP=OA,
∴∠A=∠APO,
∵EC⊥AB,
∴∠A+∠AEC=90°,
∵∠FPE=∠FEP,∠FEP=∠AEC,
∴∠AEC=∠FPE,
∴∠OPA+∠FPA=90°,
∴OP⊥PF,
∴FP是⊙O的切线
(2)证明:∵四边形OBPD是菱形,
∴PB=OB,
∵OB=OP,
∴OP=OB=PB,
∴△OPB是等边三角形,
∴∠B=∠BOP=60°,
∴∠A=30°,
∴∠AEC=∠FEP=60°,
∴∠FPE=∠FEP=60°,
∴△FPE是等边三角形,
∵PD∥AB,
∴PD⊥EF,
∴FD=ED.
【解析】(1)连接OP,根据等腰三角形的性质得到∠A=∠APO,根据垂直的定义得到∠A+∠AEC=90°,等量代换得到∠AEC=∠FPE,于是得到OP⊥PF,根据切线的判定定理即可得到结论;(2)根据菱形的性质得到PB=OB,推出△OPB是等边三角形,得到∠B=∠BOP=60°,于是得到△FPE是等边三角形,根据等边三角形的性质即可得到结论.
【考点精析】认真审题,首先需要了解菱形的性质(菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半),还要掌握垂径定理(垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧)的相关知识才是答题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】列方程解应用题
某中学七年级![]() 两个班共105人,要去市科技博物馆进行社会大课堂活动,老师指派小明到网上查阅票价信息,小明查得票价如下表:其中七
两个班共105人,要去市科技博物馆进行社会大课堂活动,老师指派小明到网上查阅票价信息,小明查得票价如下表:其中七![]() 班不足50人,经估算,如果两个班都以班为单位购票,一共应付1140元.
班不足50人,经估算,如果两个班都以班为单位购票,一共应付1140元.
购票张数 | 每张票的价格 |
| 12 |
| 10 |
100以上 | a |
(1)两个班各有多少学生?
(2)如果两个班联合起来,作为一个团体购票,可以省300元,请求a的值.
【题目】某校七年级有400名学生,在一次生物测验后,为了解本次测验的成绩情况,从中随机取了部分学生的成绩进行统计,并绘制了如下图表:
等级 | 分数 | 频数 | 频率 |
A | 90≤x≤100 | 6 | 0.15 |
B | 80≤x<90 | 20 | a |
C | 70≤x<80 | b | 0.2 |
D | 60≤x<70 | c | 0.15 |
合计 | 1 |
请你根据以上信息,解答下列问题: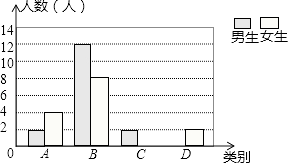
(1)a= , b= , c= , 并补全条形统计图;
(2)请你估计该校七年级共有多少名学生本次成绩不低于80分;
(3)现从样本中的A等和D等学生中各随机选取一名同学组成互助学习小组,则直接写出两名同学恰好是一名男生和一名女生的概率.