题目内容
【题目】如图,O为△ABC内一点,OD⊥AB于点D,OE⊥AC于点E,OF⊥BC于点F,若OD=OE=OF,连接OA,OB,OC,下列结论不一定正确的是( )
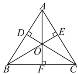
A. △BOD≌△BOF B. ∠OAD=∠OBF
C. ∠COE=∠COF D. AD=AE
【答案】B
【解析】
根据AAS推出△BOD≌△BOF和△COF≌△COE即可,由AO=AO,DO=EO根据勾股定理求出即可.
∵OD⊥AB,OE⊥AC,OF⊥BC,OD=OE=OF,
∴O在∠ABC的角平分线上(∠DBO=∠FBO),∠ODB=∠OFB=90°,
∵在△BOD和△BOF中
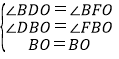
∴△BOD≌△BOF,正确,故本选项错误;
B、根据已知不能推出∠OAD=∠OBF,错误,故本选项正确;
C、∵OD⊥AB,OE⊥AC,OF⊥BC,OD=OE=OF,
∴O在∠ACB的角平分线上(∠FCO=∠ECO),∠OFC=∠OEC=90°,
∵在△COF和△COE中
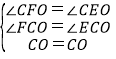
∴△COF≌△COE,
∴∠COE=∠COF,正确,故本选项错误;
D、∵OD⊥AB,OE⊥AC,
∴∠ADO=∠AEO=90°,
∵OD=OE,OA=OA,由勾股定理得:AE=AD,正确,故本选项错误;
故选B.

【题目】如图![]() ,
,![]() 平分
平分![]() ,点
,点![]() 、
、![]() 、
、![]() 分别是射线
分别是射线![]() 、
、![]() 、
、![]() 上的点(点
上的点(点![]() 、
、![]() 、
、![]() 不与点
不与点![]() 重合),联结
重合),联结![]() ,交射线
,交射线![]() 与点
与点![]() .
.
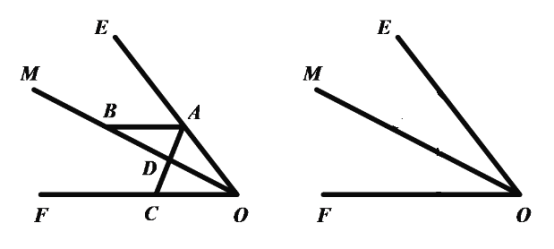
(1)如果![]() ,
,![]() 平分
平分![]() ,试判断
,试判断![]() 与射线
与射线![]() 的位置关系,试说明理由;
的位置关系,试说明理由;
(2)如果![]() ,
,![]() ,垂足为点
,垂足为点![]() ,
,![]() 中有两个相等的角,请直接写出
中有两个相等的角,请直接写出![]() 的大小.
的大小.
【题目】某校七年级有400名学生,在一次生物测验后,为了解本次测验的成绩情况,从中随机取了部分学生的成绩进行统计,并绘制了如下图表:
等级 | 分数 | 频数 | 频率 |
A | 90≤x≤100 | 6 | 0.15 |
B | 80≤x<90 | 20 | a |
C | 70≤x<80 | b | 0.2 |
D | 60≤x<70 | c | 0.15 |
合计 | 1 |
请你根据以上信息,解答下列问题: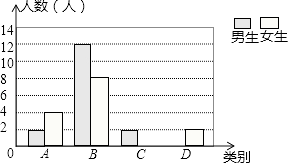
(1)a= , b= , c= , 并补全条形统计图;
(2)请你估计该校七年级共有多少名学生本次成绩不低于80分;
(3)现从样本中的A等和D等学生中各随机选取一名同学组成互助学习小组,则直接写出两名同学恰好是一名男生和一名女生的概率.