ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΕ®“εΘΚ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΆΦ–ΈG…œΒψPΘ®xΘ§yΘ©ΒΡΉίΉχ±ξy”κΤδΚαΉχ±ξxΒΡ≤νy©¹x≥ΤΈΣΒψPΒΡΓΑΉχ±ξ≤νΓ±Θ§ΕχΆΦ–ΈG…œΥυ”–ΒψΒΡΓΑΉχ±ξ≤νΓ±÷–ΒΡΉν¥σ÷Β≥ΤΈΣΆΦ–ΈGΒΡΓΑΧΊ’ς÷ΒΓ±Θ°
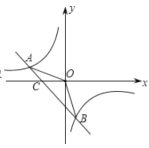
Θ®1Θ©«σΒψAΘ®2Θ§1Θ©ΒΡΓΑΉχ±ξ≤νΓ±ΚΆ≈ΉΈοœΏyΘΫ©¹x2+3x+4ΒΡΓΑΧΊ’ς÷ΒΓ±Θ°
Θ®2Θ©Ρ≥Εΰ¥ΈΚ· ΐΘΫ©¹x2+bx+cΘ®cΓΌ0Θ©ΒΡΓΑΧΊ’ς÷ΒΓ±ΈΣ©¹1Θ§ΒψB”κΒψCΖ÷±π «¥ΥΕΰ¥ΈΚ· ΐΒΡΆΦœσ”κx÷αΚΆy÷αΒΡΫΜΒψΘ§«“ΒψB”κΒψCΒΡΓΑΉχ±ξ≤νΓ±œύΒ»Θ§«σ¥ΥΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΘ°
Θ®3Θ©»γΆΦΥυ ΨΘ§Εΰ¥ΈΚ· ΐyΘΫ©¹x2+px+qΒΡΆΦœσΕΞΒψ‘ΎΓΑΉχ±ξ≤νΓ±ΈΣ2ΒΡ“Μ¥ΈΚ· ΐΒΡΆΦœσ…œΘ§ΥΡ±Ώ–ΈDEFO «ΨΊ–ΈΘ§ΒψEΒΡΉχ±ξΈΣΘ®7Θ§3Θ©Θ§ΒψOΈΣΉχ±ξ‘≠ΒψΘ§ΒψD‘Ύx÷α…œΘ§Β±Εΰ¥ΈΚ· ΐyΘΫ©¹x2+px+qΒΡΆΦœσ”κΨΊ–ΈΒΡ±Ώ”–ΥΡΗωΫΜΒψ ±Θ§«σpΒΡ»Γ÷ΒΖΕΈßΘ°
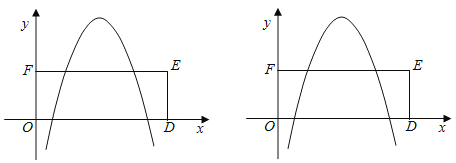
ΓΨ¥πΑΗΓΩ(1)-1,5;(2) yΘΫ©¹x2+3x©¹2ΘΜ(3) 2ΘΦpΘΦ10.
ΓΨΫβΈωΓΩ
Θ®1Θ©1-2=-1Θ§Ι ΓΑΉχ±ξ≤νΓ±ΈΣ-1Θ§y-x=-x2+3x+4-x=-Θ®x-1Θ©2+5Θ§Ι ΓΑΧΊ’ς÷ΒΓ±ΈΣ5ΘΜ
Θ®2Θ©”…Χβ“βΒΟΘΚΒψCΘ®0Θ§cΘ©Θ§Ι ΒψBΓΔCΒΡΓΑ÷Η±ξ≤νΓ±œύΒ»Θ§Ι ΒψBΘ®-cΘ§0Θ©Θ§Α―ΒψBΒΡΉχ±ξ¥ζ»κy=-x2+Θ®1-cΘ©x+cΒΟΘΚ0=-Θ®-cΘ©2+bΘ®-cΘ©+cΘ§ΫβΒΟΘΚb=1-cΘ§Ι ΘΚy=-x2+Θ®1-cΘ©x+cΘ§Ι ≈ΉΈοœΏΒΡΓΑΧΊ’ς÷ΒΓ±ΈΣ-1Θ§y-x=-x2+Θ®1-cΘ©x+c-x=-x2-cx+cΘ§Ι ![]() =-1Θ§Φ¥Ω…«σΫβΘΜ
=-1Θ§Φ¥Ω…«σΫβΘΜ
Θ®3Θ©ΓΑΉχ±ξ≤νΓ±ΈΣ2ΒΡ“Μ¥ΈΚ· ΐΈΣΘΚy=x+2Θ§Ε‘”ΎΆΦ1Θ§÷±œΏ”κΨΊ–Έ±ΏΒΡΫΜΒψΈΣΘΚΘ®1Θ§3Θ©Θ§‘ρΕ‘≥Τ÷αΈΣΘΚ-![]() =1Θ§ΫβΒΟΘΚp=2Θ§Ε‘”ΎΆΦ2Θ§Α―ΒψEΘ®7Θ§3Θ©¥ζ»κy=-Θ®x-mΘ©2+m+2≤ΔΫβΒΟΘΚm=5Μρ10Θ®…α»Ξ10Θ©Θ§Φ¥Ω…«σΫβΘ°
=1Θ§ΫβΒΟΘΚp=2Θ§Ε‘”ΎΆΦ2Θ§Α―ΒψEΘ®7Θ§3Θ©¥ζ»κy=-Θ®x-mΘ©2+m+2≤ΔΫβΒΟΘΚm=5Μρ10Θ®…α»Ξ10Θ©Θ§Φ¥Ω…«σΫβΘ°
ΫβΘΚΘ®1Θ©1©¹2ΘΫ©¹1Θ§Ι ΓΑΉχ±ξ≤νΓ±ΈΣ©¹1Θ§
y©¹xΘΫ©¹x2+3x+4©¹xΘΫ©¹Θ®x©¹1Θ©2+5Θ§Ι ΓΑΧΊ’ς÷ΒΓ±ΈΣ5ΘΜ
Θ®2Θ©”…Χβ“βΒΟΘΚΒψCΘ®0Θ§cΘ©Θ§«“ΒψBΓΔCΒΡΓΑΉχ±ξ≤νΓ±œύΒ»Θ§
Ι ΒψBΘ®©¹cΘ§0Θ©Θ§Α―ΒψBΒΡΉχ±ξ¥ζ»κyΘΫ©¹x2+bx+cΒΟΘΚ
0ΘΫ©¹Θ®©¹cΘ©2+bΘ®©¹cΘ©+cΘ§
ΫβΒΟΘΚbΘΫ1©¹cΘ§
Ι ΘΚyΘΫ©¹x2+Θ®1©¹cΘ©x+cΘ§
Ι ≈ΉΈοœΏΒΡΓΑΧΊ’ς÷ΒΓ±ΈΣ©¹1Θ§
Γύy©¹xΘΫ©¹x2+Θ®1©¹cΘ©x+c©¹xΘΫ©¹x2©¹cx+cΘ§
Ι ![]() ΘΫ©¹1Θ°
ΘΫ©¹1Θ°
ΓύcΘΫ©¹2Θ§bΘΫ3Θ§
Ι ≈ΉΈοœΏΒΡ±μ¥ο ΫΈΣΘΚyΘΫ©¹x2+3x©¹2ΘΜ
Θ®3Θ©ΓΑΉχ±ξ≤νΓ±ΈΣ2ΒΡ“Μ¥ΈΚ· ΐΈΣΘΚyΘΫx+2Θ§
ΓΏ≈ΉΈοœΏyΘΫ©¹x2+px+qΒΡΆΦœσΒΡΕΞΒψ‘ΎyΘΫx+2…œΘ§
Γύ…η≈ΉΈοœΏΒΡ±μ¥ο ΫΈΣΘΚyΘΫ©¹Θ®x©¹mΘ©2+m+2Θ§
Β±≈ΉΈοœΏ”κΨΊ–Έ”–3ΗωΫΜΒψ ±Θ§»γΆΦ1ΓΔ2Θ§
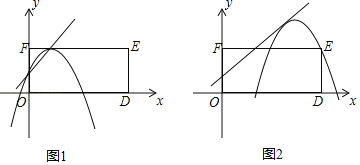
Ε‘”ΎΆΦ1Θ§÷±œΏ”κΨΊ–Έ±ΏΒΡΫΜΒψΈΣΘΚΘ®1Θ§3Θ©Θ§
‘ρΕ‘≥Τ÷αΈΣΘΚ©¹![]() ΘΫ1Θ§ΫβΒΟΘΚpΘΫ2Θ§
ΘΫ1Θ§ΫβΒΟΘΚpΘΫ2Θ§
Ε‘”ΎΆΦ2Θ§Α―ΒψEΘ®7Θ§3Θ©¥ζ»κyΘΫ©¹Θ®x©¹mΘ©2+m+2≤ΔΫβΒΟΘΚ
mΘΫ5Μρ10Θ®…α»Ξ10Θ©Θ§
Ι ©¹![]() ΘΫ5Θ§ΫβΒΟΘΚpΘΫ10Θ§
ΘΫ5Θ§ΫβΒΟΘΚpΘΫ10Θ§
Ι Εΰ¥ΈΚ·”κΨΊ–ΈΒΡ±Ώ”–ΥΡΗωΫΜΒψ ±Θ§«σpΒΡ»Γ÷ΒΖΕΈßΘΚ2ΘΦpΘΦ10Θ°

 ΧλΧλΝΖΩΎΥψœΒΝ–¥πΑΗ
ΧλΧλΝΖΩΎΥψœΒΝ–¥πΑΗ