题目内容
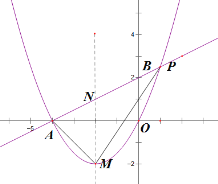
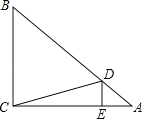
【题目】如图:三角形ABC内接于圆O,∠BAC与∠ABC的角平分线AE,BE相交于点E,延长AE交外接圆O于点D,连接BD,DC,且∠BCA=60°

(1)求∠BED的大小;
(2)证明:△BED为等边三角形;
(3)若∠ADC=30°,圆O的半径为r,求等边三角形BED的边长.
【答案】(1)60°;(2)证明见解析;(3)![]() r.
r.
【解析】
试题(1)根据三角形内角和定理求出∠BAC+∠ABC的度数,再根据角平分线定义求出∠ABE+∠BAE的度数,然后根据三角形的一个外角等于与它不相邻的两个内角的和求解;
(2)根据在同一个圆中,同弧所对的圆周角相等可得∠ADB=∠BCA=60°,再根据三角形的内角和定理求出∠DBE=60°,然后即可得证;
(3)根据∠ADC=30°可以求出∠BDC=90°,从而得到BC是圆的直径,然后求出∠ABC=30°,所以∠CBE=15°,然后求出∠DBC=45°,得到△BDC是等腰直角三角形,边长BD=![]() BC.
BC.
试题解析:(1)∵∠BCA=60°,
∴∠BAC+∠ABC=180°-∠BCA=180°-60°=120°,
∵∠BAC与∠ABC的角平分线AE,BE相交于点E,
∴∠ABE+∠BAE=![]() (∠BAC+∠ABC)=
(∠BAC+∠ABC)=![]() ×120°=60°,
×120°=60°,
∴∠BED=∠ABE+∠BAE=60°;
(2)证明:∵∠BCA=60°,
∴∠ADB=∠BCA=60°,
∴∠DBE=180°-∠BED-∠ADB=180°-60°-60°=60°,
∴△BED为等边三角形;
(3)∵∠ADC=30°,∠ADB=60°,
∴∠BDC=∠ADC+∠ADB=30°+60°=90°,
∴BC是⊙O的直径,
∵∠BCA=60°,
∴∠ABC=90°-60°=30°,
∵BE平分∠ABC,
∴∠CBE=15°,
∴∠DBC=∠DBE-∠CBE=60°-15°=45°,
∴BD=BCcos45°=2r×![]() =
=![]() r.
r.
即等边△BED的边长为![]() r.
r.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案