题目内容
【题目】如图,已知点D在⊙O的直径AB延长线上,点C在⊙O上,过点D作ED⊥AD,与AC的延长线相交于点E,且CD=DE.
(1)求证:CD为⊙O的切线;
(2)若AB=8,且BC=CE时,求BD的长.

【答案】(1)见解析;(2) 4![]() ﹣4.
﹣4.
【解析】
(1)连结0C,由AB为直径,得到∠ACB=90°,求得∠E=∠ABC,根据等腰三角形的性质得到∠ABC=∠OCB,等量代换得到∠E=∠OCB,推出OC⊥CD,于是得到结论;
(2)连接OC,由(1)得出的∠BCD=∠A,易知:∠OBC=∠CDE,由于题中告诉了BC=CE,可得到的条件是△OBC≌△DCE;因此OC=CD=6;在等腰Rt△OCD中,已知了直角边的长,即可求出斜边OD的长,进而可求出BD的长.
(1)证明:连接OC,
∵AB为直径,
∴∠ACB=90°,
∴∠BCD+∠ECD=90°,
在Rt△ADE和Rt△ABC中,∠E=90°﹣∠A,∠ABC=90°﹣∠A,
∴∠E=∠ABC,
∵OB=OC,
∴∠ABC=∠OCB,
∴∠E=∠OCB,
又∵CD=DE,
∴∠E=∠ECD,
∴∠OCB=∠ECD,
∴∠OCB+∠BCD=90°,即OC⊥CD,
∴CD为⊙O的切线.
(2)由(1)知,∠OBC=∠OCB=∠DCE=∠E,
在△OBC和△DCE中,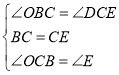 ,
,
∴△OBC≌△DCE(ASA),
∴OC=CD=6,
Rt△OCD中,OC=CD=4,∠OCD=90°,
∴OD=4![]() ,
,
即BD=OD﹣OB=4![]() ﹣4.
﹣4.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目