题目内容
【题目】如图，在长方形ABCD中，AB=6，BC=10，AE=2，连接BE、CE，线段CD上有一点H，将△EDH沿直线EH折叠，折叠后点D落在EC上的点D′处，若D′N⊥AD于点N，与EH交于点M．则①△D′MH与△CBE都是等腰三角形；②∠BEH为直角；③DH长度为
，④
；以上说法正确的个数有( )
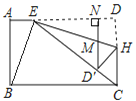
A.1个B.2个C.3个D.4个
【答案】B
【解析】
①根据两直线平行内错角相等和翻折的性质得出两底角相等证的△D′MH是等腰三角形；根据勾股定理算的
，即可证明△CBE都是等腰三角形；②根据翻折性质得出∠D′EH=∠HED，再根据两直线平行同旁内角互补得出2∠BEC+2∠D′EH=180°，最后解得∠BEH为直角；③根据△D′HC∽△DEC得出
，解得D′H，再根据翻折性质得出DH=D′H即可；④过点
做
,△ED′M与△EMN是等高三角形，
再证的△D′MF∽△CH D′，再根据相似三角形的性质即可求解.
①∵D′N⊥AD，长方形ABCD
∴
∴
根据翻折性质可得：
∴
∴△D′MH是等腰三角形
∵在长方形ABCD中，AB=6，BC=10，AE=2
∴
∴
∴
∴△CBE是等腰三角形
故①正确；
②根据翻折性质可得：∠D′EH=∠HED
∵
∴
∴
，则
∴
故②正确；
③根据翻折的性质得：
∴
∴△D′HC∽△DEC
∴，则
解得：
故③错误；
④过点做，垂直为F，如图所示：
∵
∴
∴
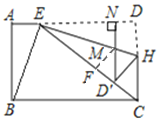
又∵
∴
∴
∴
根据翻折性质可知
∴
是
的角平分线
∴
∵△ED′M与△EMN是等高三角形
∴
故④正确
综上所述：说法正确的有2个.
故选：B.
练习册系列答案
相关题目
