题目内容
【题目】阅读材料：用配方法求最值．已知x，y为非负实数，
∵
∴
，当且仅当“x=y”时，等号成立．
示例：当x＞0时，求
的最小值．
解：
，当
，即x=1时，y的最小值为6．
（1）尝试：当x＞0时，求
的最小值．
（2）问题解决：随着人们生活水平的快速提高，小轿车已成为越来越多家庭的交通工具，假设某种小轿车的购车费用为10万元，每年应缴保险费等各类费用共计0．4万元，n年的保养、维护费用总和为
万元．问这种小轿车使用多少年报废最合算（即：使用多少年的年平均费用最少，年平均费用=
）？最少年平均费用为多少万元？
【答案】（1）x=1时，y的最小值为3．（2）n=10时，最少年平均费用为2．5万元．
【解析】
试题分析：
解：（1）
，
∴当
，即x=1时，y的最小值为3．
（2）年平均费用=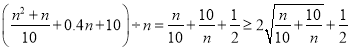
∴当
，即
时，最少年平均费用为2．5万元．
练习册系列答案
相关题目
【题目】某商店积压了100件某种商品，为使这批货物尽快脱手，该商店采取了如下销售方案，将价格提高到原来的2．5倍，再作3次降价处理；第一次降价30％，标出“亏本价”；第二次降价30％，标出“破产价”；第三次降价30%，标出“跳楼价”．3次降价处理销售结果如下表：
降价次数 | 一 | 二 | 三 |
销售件数 | 10 | 40 | 一抢而光 |
（1）跳楼价占原价的百分比是多少?
（2）该商品按新销售方案销售，相比原价全部售完，哪种方案更盈利?
