Question

【题目】小王从A地前往B地，到达后立刻返回．他与A地的距离y（千米）和所用时间x（小时）之间的函数关系如图所示．

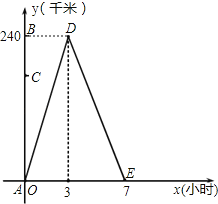
（1）小王从B地返回到A地用了多少小时？

（2）求小王出发6小时后距A地多远？

（3）在A、B之间有一C地，小王从去吋途经C地，到返回时路过C地，共用了2小时20分，求A、C 两地相距多远？

Answer 1

【答案】（1）4小时；（2）60千米；（3）160千米．

【解析】

试题分析：（1）根据函数图象即可作出回答；

（2）求得DE的解析式，然后令x=6即可求解；

（3）求得AB的解析式，小王从C到B用了n小时，列方程即可求得n的值，进而求得距离．

解：（1）从B地返回到A地所用的时间为4小时；

（2）小王出发6小时．由于6＞3，可知小王此时在返回途中，于是，设DE所在的直线的解析式为y=kx+b．

由图象可知：

解得：

∴DE的解析式是y=﹣60x+420（3≤x≤7）．

当x=6时，有y=﹣60x+420=60．

∴小王出发6小时后距A地60千米；

（3）设AD所在直线的解析式是y=mx．

由图象可知3m=240，解得m=80

∴AD所在直线的解析式是y=80x（0≤x≤3）

设小王从C到B用了n小时，则去时C与A的距离为y=240﹣80n．

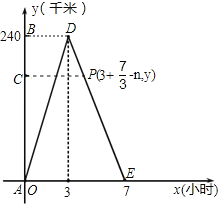
返回时，从B到C用了（﹣n）小时，

这时C与A的距离为y=﹣60[3+（﹣n）]+420=100+60n

由240﹣80n=100+60n，解得n=1

故C与A的距离为240﹣80n=240﹣80=160千米．