题目内容
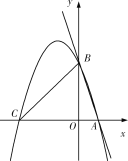
【题目】如图,已知直线y=-3x+c与x轴相交于点A(1,0),与y轴相交于点B,抛物线y=-x2+bx+c经过点A,B,与x轴的另一个交点是C.
(1)求抛物线的解析式;
(2)点P是对称轴的左侧抛物线上的一点,当S△PAB=2S△AOB时,求点P的坐标;
(3)连接BC,抛物线上是否存在点M,使∠MCB=∠ABO?若存在,请直接写出点M的坐标;若不存在,请说明理由.
【答案】(1)y=-x2-2x+3;(2)P点的坐标为(-2,3);(3)存在点M,使∠MCB=∠ABO,点M的坐标为(![]() ,
,![]() )或(-1,4).
)或(-1,4).
【解析】
(1)先把A点坐标代入y=-3x+c求出得到B(0,3),然后利用待定系数法求抛物线解析式;
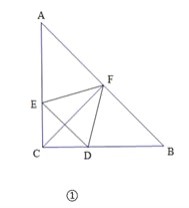
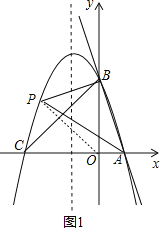
(2)连接OP,如图1,抛物线的对称轴为直线x=-1,设P(x,-x2-2x+3)(x<-1),由于S△PAB=S△POB+S△ABO-S△POA,S△PAB=2S△AOB,则S△POB-S△POA=S△ABO,讨论:当P点在x轴上方时,![]() ×3×(-x)-
×3×(-x)-![]() ×1×(-x2-2x+3)=
×1×(-x2-2x+3)=![]() ×1×3,当P点在x轴下方时,
×1×3,当P点在x轴下方时,![]() ×3×(-x)+
×3×(-x)+![]() ×1×(x2+2x-3)=
×1×(x2+2x-3)=![]() ×1×3,然后分别解方程求出x即可得到对应P点坐标;
×1×3,然后分别解方程求出x即可得到对应P点坐标;
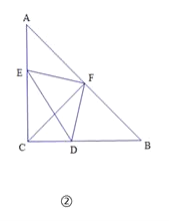
(3)解方程-x2-2x+3=0得C(-3,0),则可判断△OBC为等腰直角三角形,讨论:当∠BCM在直线BC下方时,如图2,直线CM交y轴于D,作DE⊥BC于E,设D(0,t),表示出DE=BE=![]() (3-t),接着利用tan∠MCB=tan∠ABO得到
(3-t),接着利用tan∠MCB=tan∠ABO得到![]() ,所以3
,所以3![]() -
-![]() (3-t)=
(3-t)=![]() (3-t),解方程求出t得到D点坐标,接下来利用待定系数法确定直线CD的解析式为y=
(3-t),解方程求出t得到D点坐标,接下来利用待定系数法确定直线CD的解析式为y=![]() x+
x+![]() ,然后解方程组
,然后解方程组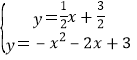 得此时M点坐标;当∠BCM在直线CB上方时,如图3,CM交直线AB于N,易得直线AB的解析式为y=-3x+3,设N(k,-3k+3),证明△ABC∽△ACN,利用相似比求出AN=
得此时M点坐标;当∠BCM在直线CB上方时,如图3,CM交直线AB于N,易得直线AB的解析式为y=-3x+3,设N(k,-3k+3),证明△ABC∽△ACN,利用相似比求出AN=![]() ,再利用两点间的距离公式得到(k-1)2+(-3k+3)2=(
,再利用两点间的距离公式得到(k-1)2+(-3k+3)2=(![]() )2,解方程求出t得N点坐标为(-
)2,解方程求出t得N点坐标为(-![]() ,
,![]() ),易得直线CN的解析式为y=2x+6,然后解方程组
),易得直线CN的解析式为y=2x+6,然后解方程组![]() 得此时M点坐标.
得此时M点坐标.
(1)把A(1,0)代入y=-3x+c得-3+c=0,解得c=3,则B(0,3),
把A(1,0),B(0,3)代入y=-x2+bx+c得![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y=-x2-2x+3;
(2)连接OP,如图1,
抛物线的对称轴为直线x=-![]() =-1,
=-1,
设P(x,-x2-2x+3)(x<-1),
S△PAB=S△POB+S△ABO-S△POA,
∵S△PAB=2S△AOB,
∴S△POB-S△POA=S△ABO,
当P点在x轴上方时,![]() ×3×(-x)-
×3×(-x)-![]() ×1×(-x2-2x+3)=
×1×(-x2-2x+3)=![]() ×1×3,解得x1=-2,x2=3(舍去),此时P点坐标为(-2,3);
×1×3,解得x1=-2,x2=3(舍去),此时P点坐标为(-2,3);
当P点在x轴下方时,![]() ×3×(-x)+
×3×(-x)+![]() ×1×(x2+2x-3)=
×1×(x2+2x-3)=![]() ×1×3,,解得x1=-2(舍去),x2=3(舍去),
×1×3,,解得x1=-2(舍去),x2=3(舍去),
综上所述,P点坐标为(-2,3);
(3)存在.
当y=0时,-x2-2x+3=0,解得x1=-1,x2=-3,则C(-3,0),
∵OC=OB=3,
∴△OBC为等腰直角三角形,
∴∠OBC=∠OCB=45°,BC=3![]() ,
,
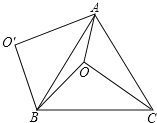
当∠BCM在直线BC下方时,如图2,直线CM交y轴于D,作DE⊥BC于E,设D(0,t),
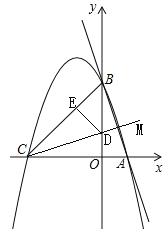
∵∠DBE=45°,
∴△BDE为等腰直角三角形,
∴DE=BE=![]() BD=
BD=![]() (3-t),
(3-t),
∵∠MCB=∠ABO,
∴tan∠MCB=tan∠ABO,
∴![]() ,即CE=3DE,
,即CE=3DE,
∴3![]() -
-![]() (3-t)=
(3-t)=![]() (3-t),解得t=
(3-t),解得t=![]() ,则D(0,
,则D(0,![]() ),
),
设直线CD的解析式为y=mx+n,
把C(-3,0),D(0,![]() )代入得
)代入得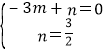 ,解得
,解得![]() ,
,
∴直线CD的解析式为y=![]() x+
x+![]() ,
,
解方程组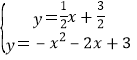 得
得![]() 或
或![]() ,此时M点坐标为(
,此时M点坐标为(![]() ,
,![]() );
);
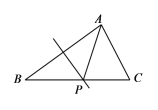
当∠BCM在直线CB上方时,如图3,CM交直线AB于N,
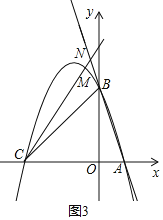
易得直线AB的解析式为y=-3x+3,AB=![]() ,AC=4
,AC=4
设N(k,-3k+3),
∵∠MCB=∠ABO,∠CBO=∠OCB,
∴∠NCA=∠ABC,
而∠BAC=∠CAN,
∴△ABC∽△ACN,
∴AB:AC=AC:AN,即![]() :4=4:AN,
:4=4:AN,
∴AN=![]() ,
,
∴(k-1)2+(-3k+3)2=(![]() )2,
)2,
整理得(k-1)2=![]() ,解得k1=
,解得k1=![]() (舍去),k2=-
(舍去),k2=-![]() ,
,
∴N点坐标为(-![]() ,
,![]() ),
),
易得直线CN的解析式为y=2x+6,
解方程组![]() ,得
,得![]() 或
或![]() ,此时M点坐标为(-1,4),
,此时M点坐标为(-1,4),
综上所述,满足条件的M点的坐标为(![]() ,
,![]() )或(-1,4).
)或(-1,4).
综上所述,存在点M,使∠MCB=∠ABO,点M的坐标为(![]() ,
,![]() )或(-1,4).
)或(-1,4).

 名校课堂系列答案
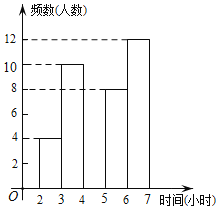
名校课堂系列答案【题目】某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) | 频数(人数) | 频率 |
2≤t<3 | 4 | 0.1 |
3≤t<4 | 10 | 0.25 |
4≤t<5 | a | 0.15 |
5≤t<6 | 8 | b |
6≤t<7 | 12 | 0.3 |
合计 | 40 | 1 |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?