Question

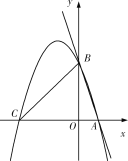
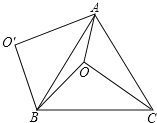
【题目】如图，O是等边△ABC内一点，OA＝6，OB＝8，OC＝10，将线段BO以点B为旋转中心逆时针旋转60°得到线段BO'，下列结论：①△BO'A可以由△BOC绕点B逆时针旋转60°得到；②点O与O'的距离为8；③四边形AOBO'的面积为24+15； ④∠AOB＝150°；⑤s△AOC+S△AOB＝9+24，其中正确的结论是_____．

Answer 1

【答案】①②④⑤．

【解析】

①证明△BO′A≌△BOC即可说明△BO'A可以由△BOC绕点B逆时针旋转60°得到；

②根据旋转的性质可知△BOO′是等边三角形，则点O与O'的距离为8，②正确；

③利用：四边形AOBO'的面积＝等边△BOO′面积+Rt△AOO′面积，进行计算即可判断；

④∠AOB＝∠AOO′+∠BOO′＝90°+60°＝150°，④正确；

⑤模仿原图的旋转方法，将线段，AO以点A为旋转中心顺时针旋转60°得到线段AO'，连接OO′，根据△AOC面积+△AOB面积＝四边形AO′BO面积＝△AOO′面积+△BOO′即可判断．

在△BO′A和△BOC中，BO’=BO,∠O’BA=∠OBA,BA=BC

∴△BO′A≌△BOC（SAS）．

∴O′A＝OC．

∴△BO'A可以由△BOC绕点B逆时针旋转60°得到，①正确；

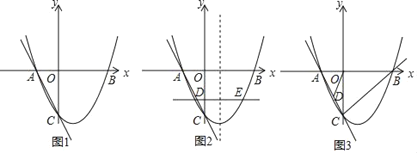
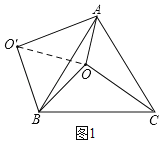
如图1，连接OO′，根据旋转的性质可知△BOO′是等边三角形，

∴点O与O'的距离为8，②正确；

在△AOO′中，AO＝6，OO′＝8，AO′＝10，

∴△AOO′是直角三角形，∠AOO′＝90°．

∴Rt△AOO′面积为×6×8＝24，

又等边△BOO′面积为×8×4＝16，

∴四边形AOBO'的面积为24+16，③错误；

∠AOB＝∠AOO′+∠BOO′＝90°+60°＝150°，④正确；

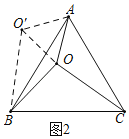
如图2，将线段，AO以点A为旋转中心顺时针旋转60°得到线段AO'，连接OO′，

则△AO′B≌△AOC（SAS），

△BOO′是直角三角形，∠BOO′＝90°，

△AOO′是等边三角形，

所以△AOC面积+△AOB面积＝四边形AO′BO面积＝△AOO′面积+△BOO′＝9+24，⑤正确．

故答案为①②④⑤．