题目内容
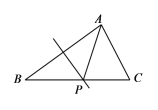
【题目】如图,在![]() 中,
中,![]() .
.
⑴已知线段AB的垂直平分线与BC边交于点P,连结AP,求证:![]() ;
;
⑵以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连结AQ,若![]() ,求
,求![]() 的度数.
的度数.

【答案】(1)见解析;(2)∠B=36°.
【解析】
(1)根据垂直平分线的性质,得到PA=PB,再由等腰三角形的性质得到∠PAB=∠B,从而得到答案;
(2)根据等腰三角形的性质得到∠BAQ=∠BQA,设∠B=x,由题意得到等式∠AQC=∠B+∠BAQ=3x,即可得到答案.
(1)证明:因为点P在AB的垂直平分线上,
所以PA=PB,
所以∠PAB=∠B,
所以∠APC=∠PAB+∠B=2∠B.
(2)根据题意,得BQ=BA,
所以∠BAQ=∠BQA,
设∠B=x,
所以∠AQC=∠B+∠BAQ=3x,
所以∠BAQ=∠BQA=2x,
在△ABQ中,x+2x+2x=180°,
解得x=36°,即∠B=36°.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目