题目内容
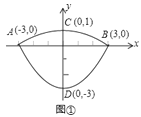
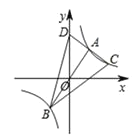
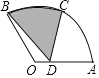
【题目】在△ABC中,有![]() ,如图, △DEF的三个顶点D,E,F分别在△ABC的边BC,AC,AB上.
,如图, △DEF的三个顶点D,E,F分别在△ABC的边BC,AC,AB上.
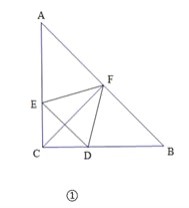
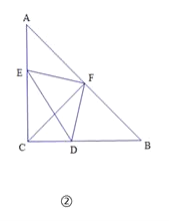
(1)已知点F是AB的中点.
①如图①,若△DEF是等边三角形,试直接写出正△DEF的边长;
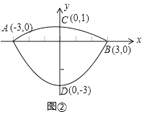
②如图②,若![]() , △DEF 的面积为10,求CD的长;
, △DEF 的面积为10,求CD的长;
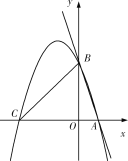
(2)若![]() ,DF=DE, △DEF的面积是否存在最小值?若存在,求此时CD的值;若不存在,请说明理由.
,DF=DE, △DEF的面积是否存在最小值?若存在,求此时CD的值;若不存在,请说明理由.
【答案】(1)①![]() ;②CD=2或6;(2)
;②CD=2或6;(2)![]()
【解析】
(1)①作FG⊥BC交BC于点G,由题可得:CF垂直平分DE、AB,设CE=CD=a,由勾股定理得DE=DF=![]() a,根据 等腰直角三角形性质得CG=BG=FG=4,DG=4-a,在Rt△FGD中,由勾股定理得一元二次方程,解之可得a值,从而可得等边三角形△DEF边长;
a,根据 等腰直角三角形性质得CG=BG=FG=4,DG=4-a,在Rt△FGD中,由勾股定理得一元二次方程,解之可得a值,从而可得等边三角形△DEF边长;
②根据等腰直角三角形性质和等量代换得∠AFE=∠CFD,由相似三角形判定和性质得![]() =1,即EF=DF,AF=CD,设CD=AF=x,则CE=8-x,由等腰直角三角形面积公式求得EF=DF=2
=1,即EF=DF,AF=CD,设CD=AF=x,则CE=8-x,由等腰直角三角形面积公式求得EF=DF=2![]() , 在Rt△EFD中,根据勾股定理得DE=2
, 在Rt△EFD中,根据勾股定理得DE=2![]() , 在Rt△EFD中,根据勾股定理列出方程解之得CD长.
, 在Rt△EFD中,根据勾股定理列出方程解之得CD长.
(2)设CD=x,则BD=8-x,根据等腰直角三角形性质和等量代换得∠AEF=∠BFD,由相似三角形判定和性质得![]() , 从而可得AF=8
, 从而可得AF=8![]() -
-![]() x,BF=
x,BF=![]() x,AE=2x,CE=8-2x,在Rt△CED中,根据勾股定理求得DE2=5x2-32x+64,由三角形面积公式得S△DEF=
x,AE=2x,CE=8-2x,在Rt△CED中,根据勾股定理求得DE2=5x2-32x+64,由三角形面积公式得S△DEF=![]() DE·DF=
DE·DF=![]() , 由二次函数性质可得△DEF的面积存在最小值及CD的长.
, 由二次函数性质可得△DEF的面积存在最小值及CD的长.
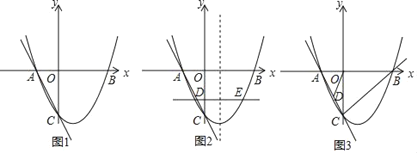
(1)解:①作FG⊥BC交BC于点G,如图:
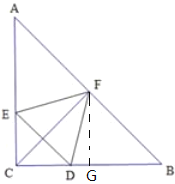
由题可得:CF垂直平分DE、AB,
设CE=CD=a,
∵∠ACB=90°,
∴DE=![]() a,
a,
∵△DEF是等边三角形,
∴DF=![]() a,
a,
∵FG⊥BC,CA=CB=8,
∴CG=BG=FG=4,DG=4-a,
在Rt△FGD中,
∴FD2=DG2+FG2 ,
即(![]() a)2=(4-a)2+42 ,
a)2=(4-a)2+42 ,
解得:a=4![]() -4,
-4,
∴DE=![]() a=
a=![]() ,
,
∴等边三角形△DEF边长为![]() ;
;
②如图2
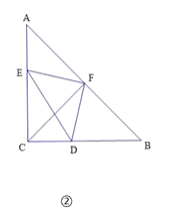
∵∠ACB=90°,CA=CB,点F时AB中点,
∴CF⊥AB,CF=AF,∠A=∠BCF=45°,
即∠AFE+∠EFC=90°,
∵∠EFD=90°,
即∠CFD+∠EFC=90°,
∴∠AFE=∠CFD,
在△AEF和△CDF中,
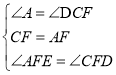
∴△AEF≌△CDF(ASA),
∴EF=DF,AF=CD,
设CD=AF=x,
∵AC=8,
∴CE=8-x,
又∵∠EFD=90°,
∴S△EFD=![]() ·EF·DF=10,
·EF·DF=10,
∴EF=DF=2![]() ,
,
在Rt△EFD中,
∴DE=![]() ,
,
在Rt△EFD中,
∵EC2+CD2=ED2 ,
∴(8-x)2+x2=40,
即(x-2)(x-6)=0,
解得:x=2,或x=6,
∴CD=2或6.
(2)解:设CD=x,则BD=8-x,
∵CA=CB=8,∠ACB=90°,
∴∠A=∠B=45°,AB=8![]() ,
,
又∵DE=DF,∠EDF=90°,
∴∠DEF=∠DFE=45°,EF=![]() DF,
DF,
∴∠AEF+∠AFE=135°,∠BFD+∠AFE=135°,
∴∠AEF=∠BFD,
∴△AFE∽△BDF,
∴![]() ,
,
∴AF=![]() BD=
BD=![]() (8-x)=8
(8-x)=8![]() -
-![]() x,BF=AB-AF=
x,BF=AB-AF=![]() x,
x,
∴AE=![]() BF=2x,CE=CA-AE=8-2x,
BF=2x,CE=CA-AE=8-2x,
在Rt△CED中,
∴DE2=CE2+CD2 ,
即DE2=x2+(8-2x)2=5x2-32x+64,
∴S△DEF=![]() ·DE·DF=
·DE·DF=![]() DE2,
DE2,
=![]() ,
,
=![]() ,
,
当且仅当![]() 时,△DEF的面积存在最小值,且最小值为
时,△DEF的面积存在最小值,且最小值为![]() .
.
∴CD=![]() .
.