题目内容
【题目】基本模型:如图1,点A,F,B在同一直线上,若∠A=∠B=∠EFC=90°,易得△AFE~△BCF. 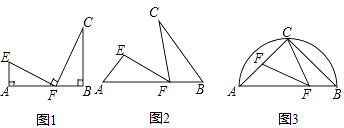
(1)模型拓展:如图2,点A,F,B在同一直线上,若∠A=∠B=∠EFC,求证:△AFE~△BCF;
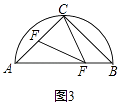
(2)拓展应用:如图3,AB是半圆⊙O的直径,弦长AC=BC=4 ![]() ,E,F分别是AC,AB上的一点,若∠CFE=45°,若设AE=y,BF=x,求y与x的函数关系式.
,E,F分别是AC,AB上的一点,若∠CFE=45°,若设AE=y,BF=x,求y与x的函数关系式.
【答案】
(1)证明:如图2,∵∠A=∠EFC,
∴∠E+∠EFA=∠EFA+∠CFB,
∴∠E=∠CFB,
∵∠A=∠B,
∴△AFE∽△BCF
(2)解:如图3,∵AB是⊙O的直径,
∴∠ACB=90°,
∴AB= ![]() =8,
=8,
∵AC=BC,
∴∠A=∠B=45°,
∴∠A=∠B=∠CFE=45°,
由(1)可得△AFE∽△BCF,
∴ ![]() ,
,
即 ![]() ,
,
∴y=﹣ ![]() x2+
x2+ ![]() x(0≤x≤8),
x(0≤x≤8),
【解析】(1)利用已知得出∠E=∠CFB,进而利用相似三角形的判定方法得出即可;(2)利用(1)得出△AFE∽△BCF,则 ![]() ,进而求出y与x的函数关系式.
,进而求出y与x的函数关系式.

练习册系列答案
相关题目