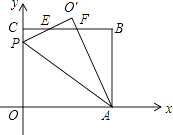
��Ŀ����
����Ŀ����֪��A�������϶�Ӧ����Ϊa����B�������϶�Ӧ����Ϊb����|a+3|+|b-2|=0��A,B ֮��ľ����Ϊ|AB|.��ش����⣺
(1)ֱ��д��a,b, |AB|��ֵ. a= ��b = �� |AB|= ��
(2)���P�������϶�Ӧ����Ϊx����|PA|-|PB|=2ʱ����x��ֵ��
(3)����P�ڵ�A����࣬M��N�ֱ���PA��PB���е�.����P�ڵ�A������ƶ�ʱ��ʽ��|PN|-|PM|��ֵ�Ƿ����ı䣿�����䣬�������ֵ���������仯����˵������.
���𰸡�(1)a=-3,b=2,|AB|=5;(2)x=![]() ;(3) ����ı�,���ɼ�����
;(3) ����ı�,���ɼ�����
��������
��1������|a+3|+��b-2��2=0���������a��b��ֵ���Ӷ�������õ�A��B��ʾ�����������|AB|��ֵ��
��2��Ӧ���ǵ�A��B��P����֮���λ�ù�ϵ�Ķ��ֿ��ܽ��⣬Ҫ�������ۣ�
��3�������е�����ת���߶�֮��ı��ֹ�ϵ�ó���
��1��a= -3 ��b= 2 �� ![]() = 5 ��
= 5 ��
��2������P�ڵ�A���ʱ��
![]()
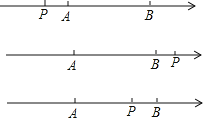
����![]() �ڵ�
�ڵ�![]() �Ҳ�ʱ��
�Ҳ�ʱ��
![]()
��������������ĵ�P�����ڣ�
����P��A��B֮��ʱ��
��-3��x��2��
![]()
![]()
![]()
![]() (x+3)-(2-x)=2��
(x+3)-(2-x)=2��
��ã�x=![]()
��3������ı䣻
��M��N�ֱ���PA��PB���е㣬
��![]() ,
,![]()
������P�ڵ�A����࣬
��![]()
��![]() ��ֵ���ᷢ���ı�.
��ֵ���ᷢ���ı�.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�