题目内容
【题目】如图,过⊙O外一点P向⊙O作两条切线,切点分别为A,B,若⊙O半径为2,∠APB=60°,则图中阴影部分的面积为 . 
【答案】4 ![]() ﹣
﹣ ![]() π
π
【解析】解:连接OA、OB,OP,如图, 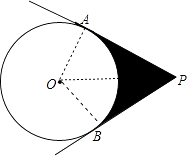
∵PA,PB是⊙O的两条切线,
∴OA⊥AP,OB⊥PB,OP平分∠APB,
∴∠PAO=∠PBO=90°,∠APO= ![]() ×60°=30°,
×60°=30°,
∴∠AOB=180°﹣∠APB=180°﹣60°=120°,
在Rt△PAO中,∵OA=2,∠APO=30°,
∴AP= ![]() OA=2
OA=2 ![]() ,
,
∴S△PAO= ![]() ×2×2
×2×2 ![]() =2
=2 ![]() ,
,
∴阴影部分的面积=S四边形AOBP﹣S扇形AOB
=2×2 ![]() ﹣
﹣ ![]() =4
=4 ![]() ﹣
﹣ ![]() π.
π.
所以答案是:4 ![]() ﹣
﹣ ![]() π.
π.
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径,以及对扇形面积计算公式的理解,了解在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).

练习册系列答案
相关题目
【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.