题目内容
【题目】在平面直角坐标系中，点P的坐标为（a，b），点P的“变换点”P`的坐标定义如下：当
时，P`点坐标为（a，－b）；当
时，P`点坐标为（b，－a）。线段l：
上所有点按上述“变换点”组成一个新的图形，若直线
与组成的新的图形有两个交点，则k的取值范围是（ ）
A. 
B. 
或
C. 
D. 
【答案】A
【解析】
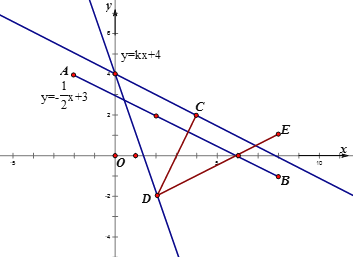
根据题意画出图形，确定变换分界点，根据条件，从直线y=kx+4的变动范围确定k的取值范围.
由a≥b,得x≥
,解得x≥2,
所以，线段变换的分界点是（2，2）
当a≥b,变换得到新图形是线段DE；当a<b时，变换得到新图形是线段DC.
且D(2,-2),C(4,2),E(8,2).
直线y=kx+4与y轴相交于（0，4），如图，假如直线与新图形有两个交点，那么2<x<4,-2<y<2.
因为
，
所以，由上述可得
，
即
，
故选：A
【题目】某同学上学期的数学历次测验成绩如下表所示：
测验类别 | 平时测验 | 期中测验 | 期末测验 | ||
第1次 | 第2次 | 第3次 | |||
成绩 | 100 | 106 | 106 | 105 | 110 |
（1）该同学上学期5次测验成绩的众数为 ，中位数为 ；
（2）该同学上学期数学平时成绩的平均数为 ；
（3）该同学上学期的总成绩是将平时测验的平均成绩、期中测验成绩、期末测验成绩按照2：3：5的比例计算所得，求该同学上学期数学学科的总评成绩（结果保留整数）。
【题目】受国内外复杂多变的经济环境影响，去年1至7月，原材料价格一路攀升，义乌市某服装厂每件衣服原材料的成本y1（元）与月份x（1≤x≤7，且x为整数）之间的函数关系如下表：
月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
成本（元/件） | 56 | 58 | 60 | 62 | 64 | 66 | 68 |
8至12月，随着经济环境的好转，原材料价格的涨势趋缓，每件原材料成本y2（元）与月份x的函数关系式为y2=x+62（8≤x≤12，且x为整数）．
（1）请观察表格中的数据，用学过的函数相关知识求y1与x的函数关系式．
（2）若去年该衣服每件的出厂价为100元，生产每件衣服的其他成本为8元，该衣服在1至7月的销售量p1（万件）与月份x满足关系式p1=0.1x+1.1（1≤x≤7，且x为整数）； 8至12月的销售量p2（万件）与月份x满足关系式p2=﹣0.1x+3（8≤x≤12，且x为整数），该厂去年哪个月利润最大？并求出最大利润．
