题目内容
【题目】A、B两地相距20km,B在A的北偏东45°方向上,一森林保护中心P在A的北偏东30°和B的正西方向上,现计划修建的一条高速公路将经过AB(线段),已知森林保护区的范围在以点P为圆心,半径为4km的圆形区域内,请问这条高速公路会不会穿越保护区?为什么?(sin15°=0.259,cos15°=0.966,tan15°=0.268) 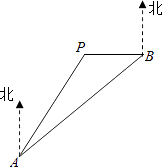
【答案】解:延长BP作BC⊥AC于C,过P作PM⊥AB于M.
因为B在A的北偏东45°方向上,
所以A在B的南偏西45°方向.
在Rt△ABC中,
∵∠CBA=∠CAB=45°,
∴AC=BC=10 ![]() .
.
在直角△PCA中,
∠PAC=30°,则PC= ![]() ,
,
∴PB=10 ![]() ﹣
﹣ ![]() ,
,
在直角△PMB中,
PM=(10 ![]() ﹣
﹣ ![]() )×
)× ![]() =10﹣
=10﹣ ![]() ≈4.226.
≈4.226.
∵4.226>4,
∴这条高速铁路不会穿越保护区.
【解析】过P作PM⊥AB于M,延长BP作BC⊥AC于C.在直角△APC中,运用三角函数用求出AC,BC的长.在直角△PCA中,运用三角函数求出PC的长,从而得到PB的长.在直角△PMB中,运用三角函数求出PM,比较PM与4km的大小关系即可.
【考点精析】根据题目的已知条件,利用关于方向角问题的相关知识可以得到问题的答案,需要掌握指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角.

练习册系列答案
相关题目