题目内容
已知A、B在直线l的同侧，自A、B向l作垂线，垂足分别为M、N，且AM=8，BN=6，MN=16，在线段MN上取一点C，使得△AMC与△BNC相似，求MC的值．
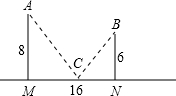
∵AM⊥MN，BN⊥MN，
∴∠AMN=∠BNM=90°，
∵AM=8，BN=6，MN=16，
设MC=x，BN=16-x，
若△AMC∽△BNC，
则
=
，
∴
=
，
解得：x=
，
若△AMC∽△CNB，
则
=
，
即
=
，
解得：x=12或x=4，
∴MC的值为：
或12或4．
∴∠AMN=∠BNM=90°，
∵AM=8，BN=6，MN=16，
设MC=x，BN=16-x，
若△AMC∽△BNC，
则
| AM |
| BN |
| MC |
| NC |
∴
| 8 |
| 6 |
| x |
| 16-x |
解得：x=
| 48 |
| 7 |
若△AMC∽△CNB，
则
| AM |
| CN |
| MC |
| BN |
即
| 8 |
| 16-x |
| x |
| 6 |
解得：x=12或x=4，
∴MC的值为：
| 48 |
| 7 |
练习册系列答案
华东师大版一课一练系列答案
孟建平名校考卷系列答案
相关题目
AB=1，一束光线从点P发射至BC上P1点，且∠BPP1=60O，经P1反射后落在AC上的P2处，则P1 P2= ，光线依次经BC反射，AC反射，AB反射…一直继续下去。当光线第一次回到点P时,这束光线所经过的路线的总长为 
重合），过动点P作PD
点A不重合），BP与AC相交于点E，设AP=x．
