题目内容
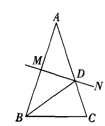
如图,正三角形ABC的三边表示三面镜子,BP= AB=1,一束光线从点P发射至BC上P1点,且∠BPP1=60O,经P1反射后落在AC上的P2处,则P1 P2= ,光线依次经BC反射,AC反射,AB反射…一直继续下去。当光线第一次回到点P时,这束光线所经过的路线的总长为
AB=1,一束光线从点P发射至BC上P1点,且∠BPP1=60O,经P1反射后落在AC上的P2处,则P1 P2= ,光线依次经BC反射,AC反射,AB反射…一直继续下去。当光线第一次回到点P时,这束光线所经过的路线的总长为 
 AB=1,一束光线从点P发射至BC上P1点,且∠BPP1=60O,经P1反射后落在AC上的P2处,则P1 P2= ,光线依次经BC反射,AC反射,AB反射…一直继续下去。当光线第一次回到点P时,这束光线所经过的路线的总长为
AB=1,一束光线从点P发射至BC上P1点,且∠BPP1=60O,经P1反射后落在AC上的P2处,则P1 P2= ,光线依次经BC反射,AC反射,AB反射…一直继续下去。当光线第一次回到点P时,这束光线所经过的路线的总长为 
2、9
解: BP=
BP= AB=1,∠BPP1=60O,∴PP′=AP2,
AB=1,∠BPP1=60O,∴PP′=AP2, P1 P2=P2C=2,
P1 P2=P2C=2,
根据等边三角形的性质可知当光线第一次回到点P时,这束光经过了三圈反射,
∴当第一次回到点P时,这束光线所经过的路线的总长为1+2+1+2+1+2=9。
 BP=
BP= AB=1,∠BPP1=60O,∴PP′=AP2,
AB=1,∠BPP1=60O,∴PP′=AP2, P1 P2=P2C=2,
P1 P2=P2C=2,根据等边三角形的性质可知当光线第一次回到点P时,这束光经过了三圈反射,
∴当第一次回到点P时,这束光线所经过的路线的总长为1+2+1+2+1+2=9。

练习册系列答案
相关题目

 ”,应先假设这个三角形中
”,应先假设这个三角形中
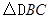 中,
中,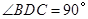 ,
, 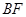 平分
平分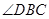 ,与
,与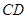 相交于点
相交于点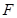 ,延长
,延长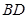 到
到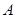 ,使
,使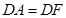 ,延长
,延长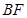 交
交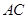 于
于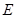 ,
,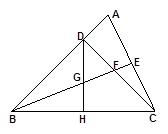
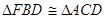 ;
;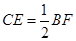 ;
;