题目内容
【题目】（问题背景）
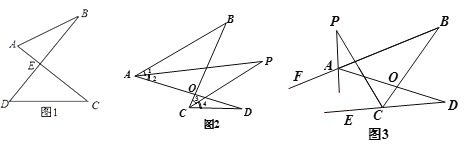
（1）如图1的图形我们把它称为“8字形”，请说明∠A+∠B=∠C+∠D；
（简单应用）
（2）如图2， AP、CP分别平分∠BAD． ∠BCD，若∠ABC=46°，∠ADC=26°，求∠P的度数；
（问题探究）
（3）如图3，直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，若∠ABC=36°，∠ADC=16°，请猜想∠P的度数，并说明理由．
（拓展延伸）
（4） ①在图4中，若设∠C=α，∠B=β，∠CAP=
∠CAB，∠CDP=∠CDB，试问∠P与∠C、∠B之间的数量关系为： （用α、β表示∠P）；
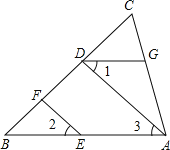
②在图5中，AP平分∠BAD，CP平分∠BCD的外角∠BCE， 猜想∠P与∠B、∠D的关系，直接写出结论．
【答案】（1）见解析；（2）36°；（3）26°，理由见解析；（4）①∠P=
②∠P=
【解析】
（1）根据三角形内角和定理即可证明；
（2）直接利用（1）中的结论两次，两式相加，然后根据角平分线的性质求解即可；
（3）由AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，推出∠1=∠2，∠3=∠4，推出∠PAD=180°﹣∠2，∠PCD=180°﹣∠3，由∠P+（180°﹣∠1）=∠D+（180°﹣∠3），∠P+∠1=∠B+∠4，推出2∠P=∠B+∠D，即可解决问题．
（4）①同法利用（1）种的结论列出方程即可解决问题．
②同法利用（1）种的结论列出方程即可解决问题．
（1）在△AEB中，∠A+∠B+∠AEB=180°．
在△CED中，∠C+∠D+∠CED=180°．
∵∠AEB=∠CED，
∴∠A+∠B=∠C+∠D；
（2）由（1）得：∠1+∠B=∠3+∠P，∠4+∠D=∠2+∠P，
∴∠1+∠B+∠4+∠D =∠3+∠P+∠2+∠P．
∵∠1=∠2，∠3=∠4，
∴2∠P=∠B+∠D=46°+26°=72°，
∴∠P=36°．
（3）∠P=26°，理由是：如图3：
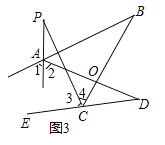
∵AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，
∴∠1=∠2，∠3=∠4，
∴∠PAD=180°﹣∠2，∠PCD=180°﹣∠3．
∵∠PAB=∠1，∠P+∠PAB =∠B+∠4，
∴∠P+∠1=∠B+∠4．
∵∠P+（180°﹣∠2）=∠D+（180°﹣∠3），
∴2∠P=∠B+∠D，
∴∠P=
（∠B+∠D）=×（36°+16°）=26°．
（4）①设∠CAP=m，∠CDP=n，则∠CAB=3m，，∠CDB=3n，
∴∠PAB=2m，∠PDB=2n．
∵∠C+∠CAP=∠P+∠PDC，∠P+∠PAB=∠B+∠PDB，
∵∠C=α，∠B=β，
∴α+m=∠P+n，∠P+2m=β+2n，
∴α－∠P = n－m，∠P－β=2n－2m=2（n－m），
∴2α+β=3∠P
∴∠P=．
故答案为：∠P=．
②设∠BAP=x，∠PCE=y，则∠PAO=x，∠PCB=y．
∵∠PAO+∠P=∠PCD+∠D，∠B+∠BAO=∠OCD+∠D，
∴x+∠P=180°－y+∠D，∠B+2x=180°－2y+∠D，
∴∠P=．
故答案为：∠P=．
