题目内容
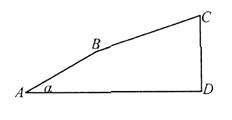
【题目】如图，小刚从点 
出发，沿着坡度为 
的斜坡向上走了650米到达点 
，且 
．
（1）则他上升的高度是 米 ；
（2）然后又沿着坡度为 
的斜坡向上走了1000米达到点 
．问小刚从 点到 点上升的高度 
是多少米（结果保留根号）?
【答案】
（1）解：如图所示：过点B作BF⊥AD于点F，过点C作CD⊥AD于点D，
由题意得：AB=650米，BC=1千米，
∴ 
= 
，
∴BF=650× 
=250米，
∴小明从A点到点B上升的高度是250米；
（2）解：∵斜坡BC的坡度为：1：3，
∴CE：BE=1：3，设CE=x，则BE=3x，
由勾股定理得： 
，
解得：x= 
，
∴CD=CE+DE=BF+CE=250+ ，
答：点C相对于起点A升高了（250+ ）米．
【解析】（1）根据题意添加辅助线，过点B作BF⊥AD于点F，过点C作CD⊥AD于点D，根据锐减三角函数的定义，在Rt△ABF中，求出小明从A点到点B上升的高度（即BF的长）。
（2）由斜坡BC的坡度，得出CE：BE=1：3，设CE=x，则BE=3x，根据勾股定理建立方程求出CE的长，然后再求出CD的长即可。
【考点精析】通过灵活运用锐角三角函数的定义和解直角三角形，掌握锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)即可以解答此题．
【题目】雾霾天气严重影响市民的生活质量．在去年寒假期间，某校八年级一班的综合实践小组同学对“雾霾天气的主要成因”随机调查了所在城市部分市民．并对调查结果进行了整理．绘制了如图不完整的统计图表．观察分析并回答下列问题．
组别 | 雾霾天气的主要成因 | 百分比 |
A | 工业污染 | 45% |
B | 汽车尾气排放 | m |
C | 炉烟气排放 | 15% |
D | 其他（滥砍滥伐等） | n |
（1）本次被调查的市民共有多少人？
（2）求m、n的值，并计算图2中区域B所对应的扇形圆心角的度数；
（3）若该市有100万人口，请估计持有A、B两组主要成因的市民有多少人？
