题目内容
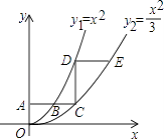
【题目】如图,平行于x轴的直线AC分别交函数y1=x2(x≥0)与y2= ![]() (x≥0)的图象于B、C两点,过点C作y轴的平行线交y1的图象于点D,直线DE∥AC,交y2的图象于点E,则
(x≥0)的图象于B、C两点,过点C作y轴的平行线交y1的图象于点D,直线DE∥AC,交y2的图象于点E,则 ![]() = .
= . 
【答案】3﹣ ![]()
【解析】解:设A点坐标为(0,a),(a>0),
则x2=a,解得x= ![]() ,
,
∴点B( ![]() ,a),
,a),
则AB= ![]()
![]() =a,
=a,
则x= ![]() ,
,
∴点C( ![]() ,a),
,a),
∵CD∥y轴,
∴点D的横坐标与点C的横坐标相同,为 ![]() ,
,
∴y1= ![]() 2=3a,
2=3a,
∴点D的坐标为( ![]() ,3a),
,3a),
∵DE∥AC,
∴点E的纵坐标为3a,
∴ ![]() =3a,
=3a,
∴x=3 ![]() ,
,
∴点E的坐标为(3 ![]() ,3a),
,3a),
∴DE=3 ![]() ﹣
﹣ ![]() ,
,
![]() =3﹣
=3﹣ ![]() .
.
所以答案是:3﹣ ![]() .
.
【考点精析】本题主要考查了二次函数的图象的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能正确解答此题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
【题目】二次函数 ![]() (a,b,c为常数,且
(a,b,c为常数,且 ![]() )中的
)中的 ![]() 与
与 ![]() 的部分对应值如表:
的部分对应值如表:
| … | -1 | 0 | 1 | 3 | … |
| … | -1 | 3 | 5 | 3 | … |
下列结论:
① ![]() ;
;
②当 ![]() 时,y的值随x值的增大而减小;
时,y的值随x值的增大而减小;
③3是方程 ![]() 的一个根;
的一个根;
④当 ![]() 时,
时, ![]() .
.
其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个