题目内容
【题目】下列条件中，不能判断△ABC是直角三角形的是（ ）
A. a：b：c＝3：4：5 B. ∠A：∠B：∠C＝3：4：5
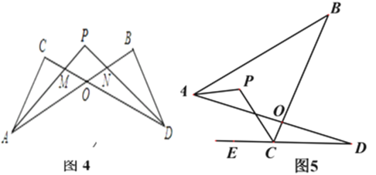
C. ∠A+∠B＝∠C D. a：b：c＝1：2：
【答案】B
【解析】
A、根据比值结合勾股定理的逆定理即可判断出三角形的形状；B、根据角的比值求出各角的度数，便可判断出三角形的形状；C、根据三角形的内角和为180度，即可计算出∠C的值；D、根据比值结合勾股定理的逆定理即可判断出三角形的形状.
A、因为a：b：c=3：4：5，所以设a=3x，b=4x，c=5x，则（3x）2+（4x）2=（5x）2，故为直角三角形，故A选项不符合题意；
B、因为∠A：∠B：∠C=3：4：5，所以设∠A=3x，则∠B=4x，∠C=5x，故3x+4x+5x=180°，解得x=15°，3x=15×3=45°，4x=15×4=60°，5x=15×5=75°，故此三角形是锐角三角形，故B选项符合题意；
C、因为∠A+∠B=∠C，∠A+∠B+∠C=180°，则∠C=90°，故为直角三角形，故C选项不符合题意；
D、因为a：b：c=1：2：
，所以设a=x，b=2x，c=x，则x2+（x）2=（2x）2，故为直角三角形，故D选项不符合题意，
故选B.
【题目】为了比较市场上甲、乙两种电子钟每日走时误差的情况，从这两种电子钟中，各随机抽取10台进行测试，两种电子钟走时误差的数据如下表（单位：秒）：
编号 类型 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
甲种电子钟 | 1 | －3 | －4 | 4 | 2 | －2 | 2 | －1 | －1 | 2 |
乙种电子钟 | 4 | －3 | －1 | 2 | －2 | 1 | －2 | 2 | －2 | 1 |
(1) 计算甲、乙两种电子钟走时误差的平均数；
(2) 计算甲、乙两种电子钟走时误差的方差；
(3) 根据经验，走时稳定性较好的电子钟质量更优．若两种类型的电子钟价格相同，请问：你买哪种电子钟？为什么？
【题目】小明同学在用描点法画二次函数y=ax2+bx+c图象时，由于粗心，他算错了一个y值，列出了下面表格：
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y=ax2+bx+c | … | 5 | 3 | 2 | 3 | 6 | … |
（1）请指出这个错误的y值，并说明理由；
（2）若点M（a，y1），N（a+4，y2）在二次函数y=ax2+bx+c图象上，且a＞﹣1，试比较y1与y2的大小．
