题目内容
【题目】如图,在矩形ABCD中,AB=1,BC=3.
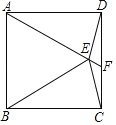
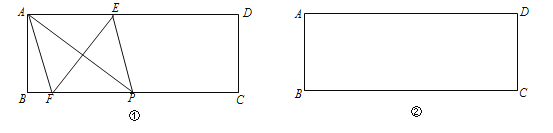
(1)在图①中,P是BC上一点,EF垂直平分AP,分别交AD、BC边于点E、F,求证:四边形AFPE是菱形;
(2)在图②中利用直尺和圆规作出面积最大的菱形,使得菱形的四个顶点都在矩形ABCD的边上,并直接标出菱形的边长.(保留作图痕迹,不写作法)
【答案】(1)见解析;(2)见解析
【解析】
(1)根据矩形的性质和EF垂直平分AP推出AF=PF=AE=PE即可判断;
(2)以矩形的一条对角线和这条对角线的垂直平分线作菱形的对角线,此时的菱形即为矩形ABCD内面积最大的菱形.
(1)证明:如图①
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠1=∠2,
∵EF垂直平分AP,
∴AF=PF,AE=PE,
∴∠2=∠3,
∴∠1=∠3,
∴AE=AF,
∴AF=PF=AE=PE,
∴四边形AFPE是菱形;
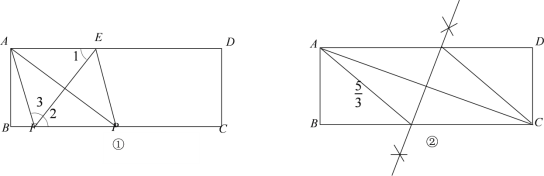
(2)如图②,以矩形的一条对角线和这条对角线的垂直平分线作菱形的对角线,连接各个点,所得的菱形即为矩形ABCD内面积最大的菱形;
此时设菱形边长为x,
则可得12+(3-x)2=x2,
解得x=![]() ,
,
所以菱形的边长为![]() .
.

练习册系列答案
相关题目