题目内容
【题目】如图所示,在⊙O上有一点C(C不与A、B重合),在直径AB上有一个动点P(P不与A、B重合).试判断PA、PC、PB的大小关系,并说明理由.
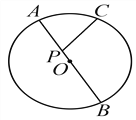
【答案】当点P在OA上时PA<PC<PB,OB上时PB<PC<PA,当点P在点O处时PA=PB=PC.
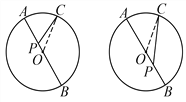
【解析】试题分析:分类讨论:当点P在点O处,易得PA=PB=PC;当点P在OA上,同样方法可得PA<PC<PB;连接OC,如图,当点P在OB上,由三角形三边的关系得到OP+OC>PC,则OA+OP>PC,所以PA>PC,再由OC=OB得到∠B=∠OCB,则∠B>∠PCB,
所以PC>PB,于是得到PB<PB<PA;
试题解析:
当点P与点O重合时,PA=PB=PC,
当点P在OA上时,PA<PC<PB.
理由:连接OC,
在△POC中,OC-OP<PC<OP+OC,
∵OA=OB=OC,
∴OA-OP<PC<OP+OB,∴PA<PC<PB,
同理,当P点在OB上时,PB<PC<PA.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
【题目】已知二次函数![]() 的图象上部分点的横坐标x与纵坐标y的对应值如下表:
的图象上部分点的横坐标x与纵坐标y的对应值如下表:
x |
|
| 0 | 1 | 2 |
|
y |
| 0 | 3 | 4 | 3 |
|
那么关于它的图象,下列判断正确的是![]()
A. 开口向上 B. 与x轴的另一个交点是![]()
C. 与y轴交于负半轴 D. 在直线![]() 的左侧部分是下降的
的左侧部分是下降的