题目内容
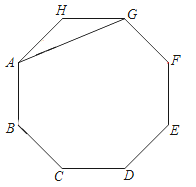
【题目】如图,AG是正八边形ABCDEFGH的一条对角线.
(1)在剩余的顶点B、C、D、E、F、H中,连接两个顶点,使连接的线段与AG平行,并说明理由;
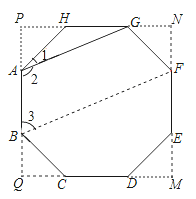
(2)两边延长AB、CD、EF、GH,使延长线分别交于点P、Q、M、N,若AB=2,求四边形PQMN的面积.
【答案】(1)BF∥AG.理由见解析;(2)![]() .
.
【解析】试题分析: (1)利用已知得出正八边形,它的内角都为135°,再利用正八边形ABCDEFGH关于直线BF对称,得出∠2+∠3=180°,进而得出答案,
(2)根据题意得出△PAH≌△QCB≌△MDE,则PA=QB=QC=MD,即PQ=QM,故四边形PQMN是正方形,进而求出PQ的长即可得出答案.
试题解析(1)连接BF,则有BF∥AG,
理由如下:
∵ABCDEFGH是正八边形,
∴它的内角都为135°,
又∵HA=HG,
∴∠1=22.5°,
从而∠2=135°﹣∠1=112.5°,
由于正八边形ABCDEFGH关于直线BF对称,
∴∠3=![]()
![]() 135°=67.5°
135°=67.5°
即∠2+∠3=180°,故BF∥AG,
(2)根据题设可知∠PHA=∠PAH=45°,
∴∠P=90°,同理可得∠Q=∠M=90°,
∴四边形PQMN是矩形.
又∵∠PHA=∠PAH=∠QBC=∠QCB=∠MDE=∠MED=45°,AH=BC=DE,
∴△PAH≌△QCB≌△MDE,
∴PA=QB=QC=MD,即PQ=QM,
故四边形PQMN是正方形.
在Rt△PAB中,
∵∠PAH=45°,AB=2,
∴ PA=AB![]() sin45°=2
sin45°=2![]() ,
,
∴ PQ=PA+AB+BQ=![]() +2+
+2+![]() =2
=2![]() +2,
+2,
故四边形PQMN的面积 =![]() =12+8
=12+8![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目