题目内容
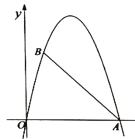
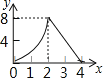
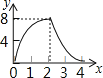
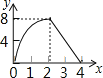
【题目】将函数y=x2﹣x﹣2的图象位于x轴下方的部分沿x轴翻折至其上方后,所得的图形是函数y=|x2﹣x﹣2|的图象,已知过点D(0,4)的直线y=kx+4恰好与y=|x2﹣x﹣2|的图象只有三个交点,则k的值为_____.
【答案】1﹣2![]() 或﹣2.
或﹣2.
【解析】
根据题意和二次函数的解析式,求出将图像进行翻折后抛物线的解析式和自变量的取值范围,将一次函数和二次函数的解析式进行联立,根据直线与抛物线的交点的个数,通过△求取k的值,然后求取交点横坐标看是否符合题意即可解决.
当y=0时,x2﹣x﹣2=0,解得x1=﹣1,x2=2,
则抛物线y=x2﹣x﹣2与x轴的交点为(﹣1,0),(2,0),
把抛物线y=x2+2x图象x轴下方的部分沿x轴翻折到x轴上方,
则翻折部分的抛物线解析式为y=﹣x2+x+2(﹣1≤x≤2),
当直线y=kx+4与抛物线y=﹣x2+x+2(﹣1≤x≤2)相切时,
直线y=kx+4与函数y=|x2﹣x﹣2|的图象恰好有三个公共点,
即﹣x2+x+2=kx+4有相等的实数解,整理得x2+(k﹣1)x+2=0,△=(k﹣1)2﹣8=0,
解得k=1±2![]() ,
,
所以k的值为1+2![]() 或1﹣2
或1﹣2![]() .
.
当k=1+2√2时,经检验,切点横坐标为x=﹣![]() <﹣1不符合题意,舍去.
<﹣1不符合题意,舍去.
当y=kx+4过(2,0)时,k=﹣2,也满足条件,
故答案为1﹣2![]() 或﹣2.
或﹣2.

练习册系列答案
相关题目
【题目】甲、乙两台机床同时加工直径为![]() 的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取
的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取![]() 件进行检测,结果如下(单位:
件进行检测,结果如下(单位:![]() ):
):
甲 |
|
|
|
|
|
乙 |
|
|
|
|
|
(1)分别求出这两台机床所加工零件直径的平均数和方差;
(2)根据所学的统计知识,你认为哪一台机床生产零件的稳定性更好一些,说明理由.